摘 要

信息时代，海量的信息资源需要被存储和提取，大规模的分布式存储系统提供了更大体系的数据存储，且成本低廉，因此越来越受工业界和学术界的重视。为确保通信网络的可靠性和稳定性，需要在系统中增加一定的冗余数据，由此我们利用到了编码的手段。目前，为系统增加冗余主要方法是复制和纠删码编码，但相比于复制存在节点的利用率不高，占用带宽较大造成资源浪费的缺点，纠删编码的方法在保证系统可靠性的同时能有效减少存储开销，因此被广泛地应用在分布式存储系统中。

纠删码本身空间复杂度和冗余度较低，能够节约存储开销，但由于存储开销和修复开销本身的矛盾性，在节点故障时，基于纠删码的分布式存储系统修复带宽较大，如何降低存储开销和修复开销成为本文的研究重点。本文从纠删码的原理出发，分析比较了纠删码和简单重复码的特点，并根据图论中著名的“最大流-最小割”理论，通过分析分布式存储系统信息流图的最小割，画出了存储开销-修复开销最优折衷曲线。最后通过分析分布式系统数据修复的模型及其性能指标，构造一种基于复制和最大距离可分码的多容错纠删码，将纠删码与分布式存储网络的底层拓扑结构相结合，同时降低系统的存储开销和修复带宽。

关键词：纠删码；分布式存储；数据修复；信息流图；拓扑结构

Abstract

In the information age, with the advancement of Internet technology, massive information In the information age, a large amount of information resources need to be stored and extracted. Large-scale distributed storage systems provide a larger system of data storage, and the cost is low, so it is increasingly valued by industry and academia. In order to ensure the reliability and stability of the communication network, it is necessary to add certain redundant data to the system, and thus we have utilized the means of coding. At present, the main method for adding redundancy to the system is to copy and erasure code coding, but the utilization of the node that is duplicated is not high, and the bandwidth is large, resulting in waste of resources. The method of erasure coding eliminates system reliability. At the same time, it can effectively reduce storage overhead, so it is widely used in distributed storage systems.

The erasure code itself has low space complexity and redundancy, which can save storage overhead. However, due to the contradiction between storage overhead and repair overhead itself, the distributed storage system based on erasure code has a large repair bandwidth when the node is faulty. How to reduce storage overhead and repair overhead has become the focus of this thesis. Based on the principle of erasure code, this thesis analyzes and compares the characteristics of erasure code and simple repetition code, and analyzes the minimum cut of information flow graph of distributed storage system according to the famous "maximum stream-minimum cut" theory in graph theory. And then draw the storage cost-repair overhead optimal compromise curve. Finally, by analyzing the model of distributed system data repair and its performance indicators, a multi-fault-tolerant erasure code based on replica and maximum distance separable code is constructed, and the erasure code is combined with the underlying topology of the distributed storage network. Reduce system storage overhead and repair bandwidth.

Keywords: erasure code；distributed storage；Information flow diagram；data repair；topology

目录

第1章 绪论 1

1.1课题背景及意义 1

1.2国内外研究现状 1

1.3论文主要研究内容 2

第2章 纠删码技术研究 3

2.1纠删码原理 3

2.2 RS纠删码及其编解码过程 4

2.3 纠删码与完全复制的比较 6

2.3.1 冗余度 6

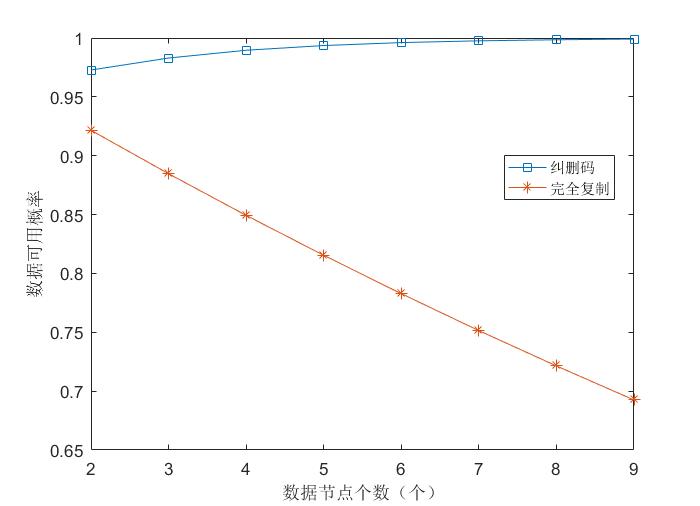
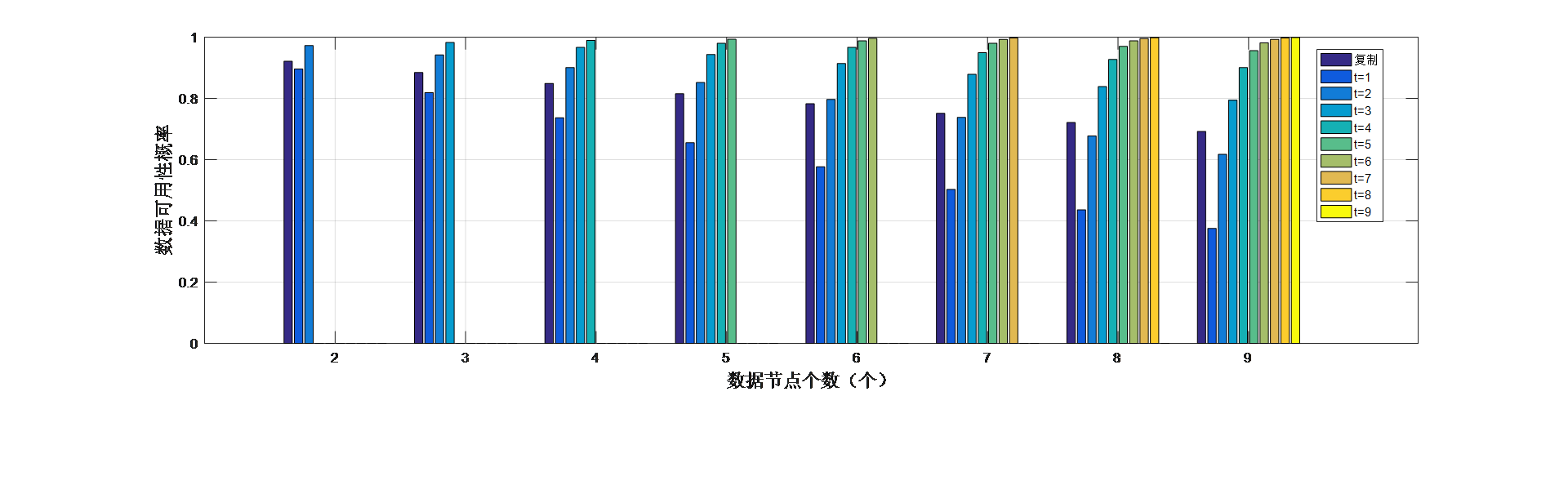
2.3.2 数据可用性和容错能力 6

2.3.3相关参数对数据可用性的影响 7

第3章 分布式存储中基于编码的数据修复 10

3.1数据修复原理分析 10

3.2存储容量和修复带宽的折衷分析 11

3.3节点修复模型 14

第4章 纠删码与网络拓扑结构结合 16

4.1 模型设计 16

4.2 模型具体描述与分析 17

第5章 总结与展望 19

5.1 总结 19

5.2 展望 19

参考文献 21

致谢 22

第1章 绪论

1.1 课题背景及意义

信息时代，随着互联网技术的进步，海量的信息资源需要被存储和提取，相比于单机存储系统小规模的存储量，大规模的分布式存储系统为更大体系的数据存储提供了解决方案。而且，目前在实践应用中的分布式存储系统还有一个重要的特点就是成本低廉，价格低廉为其能大规模使用创造了实际条件。而计算机系统中存储了许多重要的数据，日常生活中人们对于信息与网络依赖程度的提高，这给用户也带来了风险。数据是如此重要，作为数据存储的载体，存储系统的可靠性受到了极大的重视。

为确保通信网络的可靠性和稳定性，需要在系统中增加一定的冗余数据，由此我们利用到了编码的手段。目前，为系统增加冗余主要用到了两种方法，一种是基于复制的方法，这种方法虽然简单，但存在节点的利用率不高，占用带宽较大造成资源浪费等缺点；另一种是基于纠删编码的方法，这种方案在保证分布式系统可靠性与稳定性的同时能减少数据存储的存储开销，因此被广泛地应用在分布式存储系统中。

所以，分布式存储系统要应对不断增长的容量和性能需求，而规模不断增长的存储系统需要考虑存储可靠性和数据可用性的挑战，为了保证存储可靠性与数据可用性，常用的方法就是冗余，常用的冗余机制主要包括复制和纠删编码（erasure codes）。基于复制的冗余技术是将每个原始数据分块都完完本本复制到另一个设备，在原始数据失效时通过另一个设备的副本进行恢复；纠删编码最早起源于通信传输领域，通过对传输信息先进行编码再进行传输，以解决数据传输中数据丢失/损耗这一问题，由纠删编码防止数据丢失的特性，研究者将纠删码引入存储领域。

相对于传统的复制编码，纠删编码具有更高的存储效率和容错能力，在大规模存储中具有显著优势，为海量数据存储提供了高效编码方案，并且已经在一些实际的存储系统中得到了应用，如GFS，Amazon S3等。

1.2 国内外研究现状

目前，国内关于纠删码分布式存储的研究方向主要集中在两个地方，一个是磁盘阵列的研究，另一个是阵列编码的研究。如中国科学院研究生院提出一类可以纠双错的MDS阵列纠删码(V码)^[1]；南开大学则针对大规模磁盘下的阵列进行研究，探寻多容错的编码方式 ^[2]；西北工业大学针对阵列编码，对RAID布局进行分析，提出了一种可以容三错的RAID布局(TP-RAID)^[3]，除此之外，同样对于阵列编码，对于RAID-6存储系统，中国科技大学提出一种最优行对角校验恢复方法(RDOR)，可以通过最少磁盘数来完成单盘重构的过程^[4]；国防科学技术大学为大规模存储系统设计了一种高容错低修复成本的编码EXPyramid^[4]；清华大学从磁盘阵列的容错编码技术的角度出发，针对RAID-6和大规模磁盘阵列研究设计C码和GRID码^[5]，并对这种码提出一种相适应的RAID扩容方案FastScae^[6]。

纠删码存储集群相关研究则主要集中于国外大公司，从产品的角度出发，这些大公司为自己旗下大规模存储系统产品提供设计方案并不断更新优化方案。例如，谷歌在其目前的GFS文件系统中添加了RS码支持^[7]；而微软公司研制的Azure云存储系统也在此基础上进行优化，不仅添加了RS码支持^[8]，而且在RS纠删码的基础上设计了一种具有重构优化特性的编码，我们称之为局部修复码（Local Repairable Code，LRC）^[9]；而Facebook采用Mirrored RAID-5编码^[10]和RS编码来搭建其存储集群。

1.3 论文主要研究内容

本文主要研究的是基于纠删码的分布式存储系统。分析纠删码的编码及解码的原理，比较其与完全复制的不同，通过分析数据修复模型，了解存储开销和修复带宽之间的关系，构造一种多容错纠删码，将纠删码与分布式存储网络拓扑结构相结合，构造一种新模型，存储开销较小的情况下，减小数据修复的带宽消耗，达到优化系统的目的。本文主要研究内容的具体安排如下：

第1章，首先对本课题的背景及其研究的意义进行介绍，说明基于纠删码的分布式存储系统研究的必要性，然后对其国内外研究现状进行介绍，了解目前基于纠删码的分布式存储系统的主要研究方向及内容。

第2章，首先对纠删码的原理及编解码过程进行分析，然后对常用纠删码的原理进行介绍，最后基于纠删码在数据容灾模型中的应用，并分别从冗余度、数据可用性等方面比较了纠删码和简单重复码的特点，定量分析相关参数对于纠删码性能的影响。

第3章，分析纠删码在数据修复中的局限性，通过分析数据修复的编码原理和过程，对存储容量和修复带宽进行折衷分析，并探究相关参数的变化对系统性能指标的影响，最后介绍目前常用的节点修复模型。

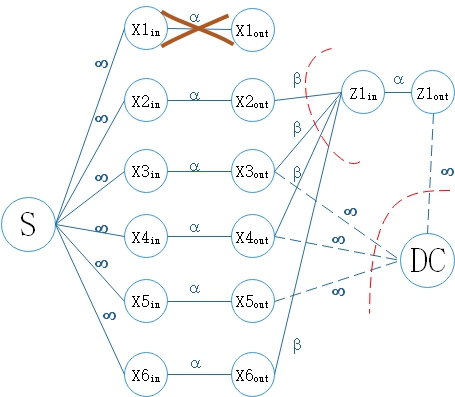
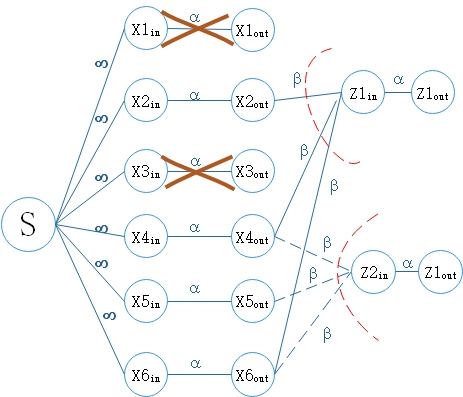
第4章，构造一种基于复制和最大距离可分码的多容错纠删码，将纠删码与分布式存储网络的底层拓扑结构相结合，研究如何快速精确地修复故障存储节点以及如何最小化存储系统的修复开销。

第5章，对本篇论文基于纠删码的分布式存储系统研究的内容及结论进行总结，最后对其未来的研究方向进行展望。

第2章 纠删码技术研究

2.1 纠删码原理

纠删码（erasure code）是一种前向错误纠正的技术，来源于通信传输领域，由于其数学特性，现在渐渐应用在大规模存储系统中，尤其是分布式存储系统中。一般是将要存储的文件分割成k块，然后对其编码，将得到的n个编码后的数据块存储在不同的节点中，纠删编码用于仅在给定n个数据块的子集的情况下根据任意k个可用的数据块就可以重构出原始文件。纠删码能够节约存储开销，但其编码方式较为复杂，需要大量计算，计算开销大，且节点故障时修复带较大。

用数学方式对纠删码原理进行较为正式的描述：纠删码一般可用数组（n, k, b, k'）来表示，在此四元组中，n表示经过纠删编码后的数据块个数，包括原始数据块和冗余数据块，而k代表编码前文件数据块的个数（即原始文件），b是指每个数据块包含的数据大小，k'表示恢复原始信息需要的数据块，k'是一个不小于k的数。在纠删码编码和解码的过程中，首先用户原始文件被分成k个数据块（消息包），从集合的角度定义为F（其中F=(F₁, F₂, …, F_k)）。每个数据块F_i(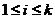)长度固定，均包含b个比特的数据量。在编码过程中，定义一个编码函数，对原始文件进行相应的编码，从编码函数中接收端需确定相应的解码规则，得到解码函数。将编码之后的文件用F’表示，其中F’定义为集合（C₁, C₂…, C_n）。需注意，编码之后的文件块C_i(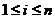)大小仍为b比特。在编码的过程中，首先选择n个向量b_i(b_i1, b_i2, …, b_ik)(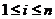)，要求这n个向量中任意k个向量线性无关，由此得到数学表达式：

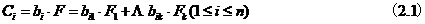
然后令集合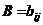，其中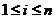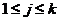，，即编码过程可表示为：

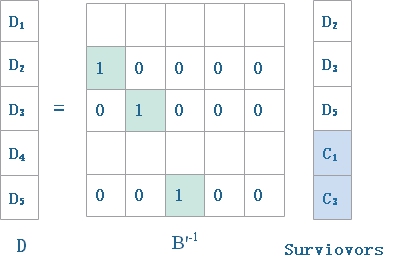
上式得到的C_i(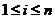)就是编码后的数据集合，可以发现其中有n-k个向量的冗余，令冗余度m=n-k,假设编码之后的数据集合C_i中的m个数据块因为某种原因失效或不可得，则需要从剩余的数据集合（k个数据块）恢复原始数据，此时用到解码函数。之前通过矩阵B对数据块进行编码，此时解码则需利用到矩阵B，不过使用前需对矩阵B进行处理，删除B矩阵中丢失数据块所对应的行，得到矩阵B₁，然后通过矩阵B₁的逆矩阵进行解码操作（矩阵B₁中任意k个向量是线性无关的，因此可逆）。解码过程可表示为：

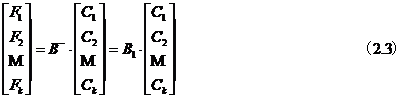
2.2 RS纠删码及其编解码过程

Reed-Solomon（RS）纠删码最初在1960年由里德（Reed）和索罗蒙（Solomon）提出，是一种在数据通信领域被广泛使用的最大距离可分码（MDS码），RS码具有最优的存储效率，且其编译算法较为简单。

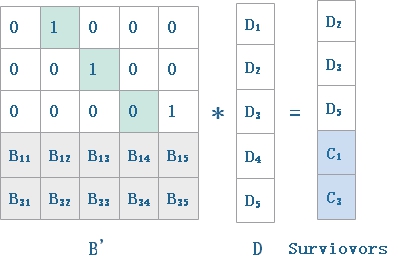
RS纠删码一般包含两个参数n和m，记为RS(n, m)，其中参数n表示原始数据块个数，参数m表示校验数据块的个数。在编码时，用原始数据块乘上一个 (n m)*n的矩阵，然后得出一个(n m)*1的矩阵，得到的矩阵，前面n个与原始矩阵相同，后面m个即为校验数据块。如图2.1，以n=5，m=3的RS纠删码为例，即此时原始数据块为5个，校验数据块为3个，经过编码可以发现结果矩阵中上半部分5个数据块的值恰好等于原始数据块，而最后3个则是计算出来的校验块。

RS码的编码过程如图2.1所示。其中D是原始数据块，C为校验块。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：