摘 要

图论是近代数学的一个重要分支，无论是在数学领域中，还是在物理、化学、生物、天文、地理、计算机、信息、经济、交通等领域中，图论都有着不可替代的应用。染色问题则是图论中亘古不衰的话题，我们生活中许多常见的问题，抽象成数学模型后都可以转为边染色问题，例如：课表安排问题，教室安排问题，化学品存储问题，交通定向问题，任务指派问题等，都可以用边染色模型的理论方法进行解决。强边染色是边染色问题的一个新兴话题，它指的是图中任意两条距离至多为2的边不着同样的颜色。强色数指的是对图进行强边染色所需最少颜色数的数目。强边染色的相关结果在通讯中频率分配等现代实际应用问题中起着理论依据的作用。

1985年，Erdös和Nešetřil提出了如下著名猜想：

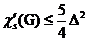若Δ是偶数

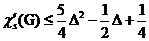若Δ是奇数

围绕这个猜想，学者们进行了广泛的研究，并证明了：当Δ不超过3时，猜想是成立的；当Δ=4时，目前得到的最好的结论是21，只比猜想的结论20多了一种颜色。本文为了研究Δ=4时图的强边染色，针对边度不超过7的平面图进行了初步研究，先证明了对边度不超过7的情况成立等价于对Δ=4，δ=3并且边度不超过7的情况成立，获得了一个更强的条件，再根据围长大小分类讨论，最终得出了边度不超过7的平面图的强色数不超过14的结论。

关键词：强边染色；强色数；平面图；最小反例法

Abstract

Graph theory is an important branch of modern mathematics. Graph theory has irreplaceable applications in mathematics, physics, chemistry, biology, astronomy, geography, computer, information, economy, transportation and other fields. Dyeing problem is an everlasting topic in graph theory. Many common problems in our life can be transformed into edge dyeing problem after abstracting into mathematical model, such as: timetable arrangement problem, classroom arrangement problem, chemical storage problem, traffic orientation problem, task assignment problem and so on, which can be solved by the theoretical method of edge dyeing model. Strong edge-coloring is a new topic in edge dyeing. It refers to that any two edges of a graph whose distance is at most 2 do not have the same color. Strong chromatic index refers to the minimum number of colors required for strong edge-coloring of a graph. The results of strong edge-coloring play a theoretical role in modern practical applications such as frequency allocation in communication.

In 1985, the following famous conjectures are put forward by Erdös and Nešetřil: 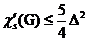if Δ is even

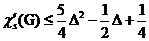if Δ is odd

Around this conjecture, scholars have conducted extensive research and proved that the conjecture is valid when a does not exceed 3; when Δ=4, the best conclusion is 21, which is only one color more than the conjecture conclusion 20. In order to study the strong edge coloring of graphs with Δ=4, this paper makes a preliminary study on planar graphs with no more than 7 edges. Firstly, it is proved that the case with no more than 7 edges is equivalent to the case with Δ=4, δ=3 and no more than 7 edges. A stronger condition is obtained. Then, the edges are classified and discussed according to the size of girth. The conclusion that the strong chromatic number of planar graphs with degree no more than 7 does not exceed 14.

Key Words：Strong edge-coloring；Strong chromatic index；Planar graphs；Minimum counter-example method

目 录

第1章 绪论 1

第2章 概念与记号 5

2.1 基本概念与记号 5

2.2 最小反例法与相关概念 6

第3章 猜想的证明 8

3.1 等价的定理 8

3.2 图G的性质 9

3.3 图G无圈的情形 12

3.4 图G围长为3情形 12

3.5 图G围长为4情形 13

3.6 图G围长为5情形 17

3.7 图G围长不少于6情形 18

3.8 总结与展望 21

参考文献 22

致 谢 24

第1章 绪论

1736年，瑞士数学家Euler通过一笔画问题，完美解决了困惑当时的人们几十年的“哥尼斯堡七桥难题”，在解决问题的过程中，一门新的数学分支——图论诞生了。如今，图论已成为数学学科一个非常重要的分支，它为诸多现代科学的方法提供了理论的支撑。

自从“四色问题”被提出后，图的染色问题就备受数学家关注。至今，染色问题已有许多分支，例如边染色，点染色，面染色，全染色等等，其中被研究的最多，结论最完善的便是边染色问题了。而强边染色则是边染色中的一个新兴话题，一些科学技术问题抽象成数学模型便成了强边染色模型，例如通讯中频率分配问题。

无线网络中的信号分配问题是将频率分配给每一对互相通信的收发器。将其抽象成数学模型后，以图中的结点代表收发器，以边代替通信渠道，我们需要将频率分配给每一条边，用不同的颜色代替不同的边，那么频率分配问题便转化为图的边染色模型。我们需要信号之间无相互干扰，有两种情形信号会相互干扰：一种是两台收发器发出相同的频率给同一台发射器，抽象成数学模型，即两条相邻的边染相同的颜色；另一种是存在一条长为3的路uvwx，u发送给v的信息频率与x发送给w的相同，这时由于w与v相邻，因此v会接受到来着u和w相同频率的信息，抽象成数学模型，即两条距离为2的边染相同的颜色。若要避免信号互相干扰，则需要对图中任何距离不超过2的两条边分配不同的颜色，于是我们需要对图进行强边染色。事实上，强边染色正是在无冲突频率分配问题的处理过程中被提出来的^[1]。

如今，强边染色问题已经有了一些成熟的方法，如贪婪染色法，最小反例法，权值转移法等。强边染色也已经有了许多成熟的结果，但是有些强边染色问题的上界仍可以降低，强边染色正处于发展中。

下面列举一些目前强边染色的国内外现状：

强边染色的概念最初是由Fouquet和Jolivet提出的^[2,3]。他们在研究中发现:

定理1.1 对于Δ=3的所有图G，都有χ_S´(G)≤2Δ²－2Δ＋1。

这个上界很快被改进，并被推广到最大度为任何正整数：

定理1.2 对于任何最大度为Δ的图G，都有χ_S´(G)≤2Δ(Δ-1)。

定理1.2实际上是Bermond猜想的一个推论^[4]。

1985年，在布拉格举行的数学家会议上，P.Erdös和J.Nešetřil提出下列猜想^[5,6]：

猜想1.1 任何图G都有：

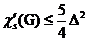若Δ是偶数

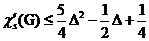若Δ是奇数

对于Δ≤3的平面图情形，有下面结论：

Andersen和Horák等人分别独立证明了^[7,8]：

定理1.3 如果平面图G满足Δ＝3，则χ_S´(G)≤10。

kostochka等人证明了^[9]：

定理1.4 如果平面图G满足Δ≤3，则χ_S´(G)≤9。

对于Δ≤4的平面图情形，有下面结论：

Horák证明了^[10]：

定理1.5 如果平面图G满足Δ≤4，则χ_S´(G)≤23。

Cranston证明了^[11]：

定理1.6 如果平面图G满足Δ＝4，则χ_S´(G)≤22。

Y. Wang等人证明了^[12]：

定理1.7 如果平面图G满足Δ＝4，则χ_S´(G)≤19。

对于Δ≥3的平面图，Faudree等人证明了下列定理^[13]：

定理1.8 如果平面图G满足Δ≥3，则χ_S´(G)≤4Δ 4。

他们同样构建了一类平面图满足Δ≥2，使得χ_S´(G)＝4Δ-4。

以上是关于平面图Δ≤4的情形，对于一般图Δ＝4，则有下列结论：

Mingfang Huang等人在中证明了^[14]：

定理1.9 如果图G满足满足Δ＝4，则χ_S´(G)≤21。

Horák, Qing和Trotter等人曾评论说^[8,15]：

对于某些ε＞0，有χ_S´(G)≤(2-ε)Δ²，这是一个非常难证明的问题。

这的确是一个十分困难的问题，到目前为止，唯一已知的上界仅仅为1.998。

Molloy和Reed在中证明了^[16]：

定理1.10 当Δ充分大时，强边色数上界不超过1.998Δ。

对于大围长的平面图，有下列结论：

定理1.11(Borodin et al.^[17]) 如果平面图G满足Δ≥3，g≥40[Δ/2]，则χ_S´(G)≤2Δ－1。

定理1.12(Chang et al.^[18]) 如果平面图G满足Δ≥4，g≥10Δ 46，则χ_S´(G)≤2Δ－1。

对于围长较小的平面图，有下列结论：

Hudák等人证明了下列结果^[19]：

定理1.13 如果平面图G满足Δ≥3，g≥6，则χ_S´(G)≤3Δ＋6。

这一结果被Bensmail等人改进到3Δ 1^[20]。

定理1.14 如果平面图G满足Δ≥3，g≥6，则χ_S´(G)≤3Δ＋1。

对于围长g≥7的情况，Ruksasakchai等人得到了一个更小的下界^[21]：

定理1.15 如果平面图G满足Δ≥3，g≥7，则χ_S´(G)≤3Δ。

对于平面图G，由定理1.4和定理1.7知：

若Δ≤3，则χ_S´(G)≤ 9

若Δ＝4，则χ_S´(G)≤19

若Δ＝3，则∀e∈E(G)，都有d(e)≤2Δ＝6，此时χ_S´(G)≤ 9；

若Δ＝4，则∀e∈E(G)，都有d(e)≤2Δ＝8，此时χ_S´(G)≤19。

边度上界为偶数的情况以及得到了证明，那么边度上界为奇数呢？

我们猜测：

猜想1.2 若∀e∈E(G)，都有d(e)≤7，则χ_S´(G)≤14。

下面围绕猜想1.2展开本论文的证明。

第2章 概念与记号

2.1 基本概念与记号

本节将介绍一些常用的图论术语以及一些本论文对一些记号的定义。

本论文所讨论的所有染色问题，都是指强边染色。对于图G，我们记V(G),E(G)分别表示图G的结点集，边集。图G可以表示为G＝lt;V(G),E(G)gt;，其中V(G)≠∅。对于图G中的结点v，如果G中有m条边以v为端点，则称v为m度结点，记作d(v)＝m；对于图G中的边e，如果e的两个端点度数分别为m₁,m₂，则称e为(m₁ m₂)度边，记作d(e)＝m₁ m₂。图G中所有结点的度数最大值与最小值，我们分别记作Δ(G),δ(G)，或分别简记为Δ,δ。如果结点u,v之间存在一条边，我们称u,v相邻，以及u是v的邻结点。结点v的所有邻结点构成的集合记作N(v)。如果边a，b有共同端点，我们称a，b相邻，以及a，b距离为1。如果a，b不相邻，但存在一条边c同时与a，b相邻，我们称a，b距离为2。除去e自身外，所有与边e距离不超过2的边构成的集合记作N₂(e)。显然有性质：设a，b是两条相异的边，若a∈N₂(b)，则b∈N₂(a)。设a，b是图G的两条边，我们记a，b的距离为D(a,b)。则N₂(e)＝{a|a∈E(G)，D(e,a)≤2，a≠e}。我们特别规定D(e,e)＝0，∀e∈E(G)。在接下来的讨论中，除非特别声明，否则我们不考虑边自身到自身距离的这种情况，即我们认为：∀a,b∈E(G)，D(a,b)≥1。

强边染色即满足下列条件的染色：∀a∈E(G)，若a∈N₂(b)，则a,b染不同的颜色。也可表述为：∀a,b∈E(G)，若边a，b染相同的颜色，则D(a,b)≥3。显然，图G的强边染色方式不唯一。对图G进行强边染色所需的最少颜色数目，我们称之为强色数，记作χ_S´(G)。显然，如果能用λ种颜色对图G进行强边染色，则必有：χ_S´(G)≤λ。

在图G中，若边e的两个端点为u,v，则可记作e=lt;u,vgt;。若lt;u,vgt;与lt;v,ugt;不等价，我们称图G为有向图，否则称为无向图。对于无向图，若e=lt;u,vgt;，可简记做e=uv或e=vu。如果任意两个结点之间至多存在一条边，我们称图G是无重边图，否则称为有重边图。

如果存在n（n≥1）条边e₁,e₂,…,e_n，使得∀i∈{1,2,…,n}：当i≠1时，D(e_i,e_i-1)＝1；当i≠n时，D(e_i,e_{i 1})＝1。我们则称e₁e₂…e_n是一条路长为n的路径，e₁,e_n的两个不属于任何e_i,e_j（1≤i＜j≤n）公共端点的结点u，v称之为路径的首尾结点。若路径e₁e₂…e_n满足：∀e∈{e₁,e₂,…,e_n}，e∈E(G)，我们称路径e₁e₂…e_n是G中的路径。当n≥3时，我们如下定义图G中任意两条边的距离：∀a,b∈E(G)，a=u₁u₂，b=v₁v₂，D(a,b)＝n等价于图G中至少存在一条以u,v为首尾结点，路长为n-1的路径，但不存在以a,b为首尾结点，路长小于n-2的路径，其中u∈{u₁,u₂}，v∈{v₁,v₂}。

对于路径e₁e₂…e_n，设其首尾结点分别为u,v，若u=v，即u与v重合，我们则称e₁e₂…e_n是一个n-圈。如果n-圈e₁e₂…e_n满足：∀e∈{e₁,e₂,…,e_n}，e∈E(G)，我们则称n-圈在G中。图G中所有圈所含边数的最小值，我们称之为G的围长，记作g(G)，或简记为g。显然，由于图G无重边，因此图G不含2-圈，即图G中最小的圈为3-圈。显然，n-圈（n≥3）把除去n-圈外的整个平面分为了2个区域，面积有限的区域称之为n-圈的内部，面积无限的区域称之为n-圈的外部。结点v∈V(G)，v位于面积有限的区域，则称v在n-圈内部；v位于面积无限的区域，则称v在n-圈外部；v位于两区域的交界，则称v在n-圈上。平面图指满足下列条件的图：∀u,v∈V(G)，如果u,v分别在一个n-圈的内部，外部，则边uv不存在（其中n-圈不需要在图G中）。