黏菌阿米巴聚集的数学模型及求解毕业论文
2020-02-14 14:51:34
摘 要
阿米巴黏菌的建模是微生物学和数学交叉领域一个非常基础也非常重要的一个问题,不仅是在研究微生物活动有广泛应用,在研究动物群体运动习性或者社会学问题方面也有一定意义。
本文介绍了阿米巴问题的生物学背景和基本概况,首先从宏观角度,针对阿米巴整体移动性质进行较简单的一维模型建模,然后推广到二维较复杂情况,对以上两种模型,获得了阿米巴和诱导物变化速率方程并讨论了方程的稳定性。而后又从微观角度针对阿米巴个体随机行走的性质进行数学建模。最终,讨论了该问题在生物学及其他学科领域的应用,并展望未来的研究方向。
关键词:Keller-Segel模型;趋化性;黏菌;稳定性分析
Abstract
Modeling of amoeba slime molds is a very basic and important problem in the field of Microbiology and mathematics. It is not only widely used in the study of microbial activities, but also significant in the study of animal movement habits or sociological problems.
This paper introduces the biological background and general situation of the amoeba problem. Firstly, from a macroscopic point of view, a simpler one-dimensional model is established for the overall mobility of amoeba, and then extended to a more complex two-dimensional situation. For the above two models, the rate equation of change of amoeba and inducer is obtained and the stability of the equation is discussed. Then, from the micro point of view, the mathematical model of the random walk of amoeba individuals is established. Finally, the application of this problem in biology and other disciplines is discussed. The future research directions are also prospected.
Key Words: Keller-Segel model, chemotaxis, slime molds, stability analysis
目录
摘要 I
Abstract II
第1章 绪论 1
1.1 研究背景 1
1.2 研究现状 2
1.3 课题研究内容及预期目标 3
第2章 宏观角度 4
2.1一维阿米巴数学模型 4
2.1.1 无诱导物情况 5
2.1.2 存在诱导物情况 7
2.1.3 稳定性分析 9
2.2.二维阿米巴数学模型 12
2.2.1浓度(密度)变化方程 13
2.2.2 稳定性分析 15
2.3 总结 16
第3章 微观角度 17
3.1 严格局部模型 17
3.2 障碍物模型 19
3.3 梯度模型 20
第4章 研究意义与应用 21
第5章 结论与未来展望 24
参考文献 25
致谢 26
第1章 绪论
1.1 研究背景
阿米巴黏菌的聚集是近年来发育生物学关注的一个重要现象,它们虽然小,但是形态形成,聚集形成跟很多高等生物无异,研究这个问题可以帮助我们了解单个细胞是发育成一个复杂胚胎的(这是胚胎学的内容),当然作为数学问题我们不会研究地那么深入,我们的目的是建立数学模型,描述阿米巴黏菌的运动和聚集。作为阿米巴的一种,盘基网柄菌(Dictyostelium discoideum)是科学家研究微生物聚集分裂现象的模式生物,因为其特殊通信交流方式,也被称为社会阿米巴[1]。
什么引发了从单一细胞生物体到复杂多细胞生物体的变化? 这个过程是如何发生的?
最开始我们要了解的是黏菌阿米巴在孢子阶段的生命周期,最开始阿米巴菌在保护层中,类似一个还未出生的过程,然后在合适的环境下,阿米巴菌便从孢子中钻出。他是一种单细胞有机体,和我们了解的其他细菌相近,他没有固定的形态,大小是微米数量级的,运动依赖鞭毛,或是说伪足爬行蠕动。
刚离开孢子时,他们会散开,就像他们之间有斥力一样,但后面又会讲到,他们又会因为食物聚集,食物耗尽时又会随机分布为群落,以一个阿米巴为中心进行移动。
阿米巴喜好污物,比如粪便,包含有机物的污水等,他们以其中的细菌为食。如果环境适宜,食物充足,阿米巴便不断进食,不断吞噬细菌,并不断有丝分裂,繁殖壮大;如果环境恶劣或者食物匮乏不足以维持,阿米巴便停留在分裂间期,无规律的蠕动,以寻求一个对自己生存繁衍更有利的区域。
这种习性就导致了阿米巴的聚集,虽然我们还没有研究出他们聚集的具体细节,但可以观察到的是在食物中断后的一段时间内,他们开始聚集在几个集中点上,有趣的是,这些集中群落的分布是有一定规律的,不是完全无规则的,他们之间总有一定的间距。
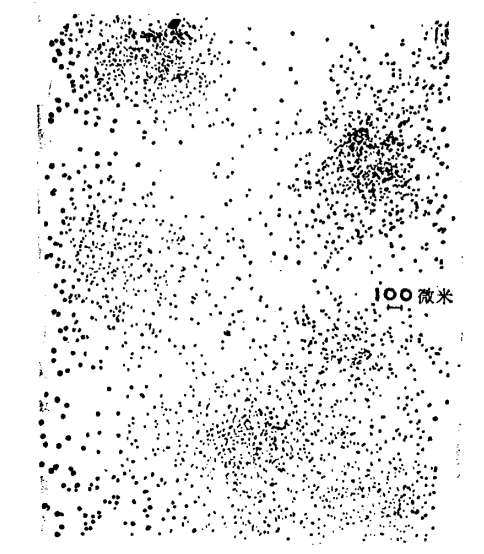
图1.1 阿米巴准备开始聚集时的布局
之后聚集于一个群落的阿米巴便形成了一个多细胞聚集体(黏菌数量根据实验的不同结果也不同),在我们的观察中他们似乎已经成为一个整体运动觅食,但事实上他们个体仍是单细胞,仍然保留着细胞壁。在一定的条件下,聚集体暂停,竖起一个囊柄,它的顶端有个圆球,包裹着孢子,之后孢子会离开囊柄,这形成了一个完整的生命周期[2]。
1.2 研究现状
现在对这个问题前人已经做出了很多工作,最著名的比如Patlak-Keller-Segel(PKS)模型,也就是本文核心讨论的模型,这种经典模型在微生物学、开发、免疫学、癌症、生态学和犯罪等多个领域的应用受到了广泛的关注。后来又有不少学者在这个模型的基础上针对不同问题提出不同的模型变体,也有人对该模型的解的性质还有稳定性做了更深入的研究。当然该问题也不只有一种模型可选,还有如Othmer-Stevens模型等。
1.3 课题研究内容及预期目标
我们关注的问题就是阿米巴为何聚集,聚集的群落有何分布规律,他们的聚集和运动一定是有规律有目的的,这是一个非常重要也是非常有价值的问题,在阿米巴上观察相较其他有机体也更明显,我们还可以为他们的聚集分裂设置一些条件观察其变化。
说到生物朝着某些物质浓度高的性质,我们可以很自然的想到趋药性(chemotaxis),是指生物对外界环境中的化学物质刺激所产生的趋向性反应,生物会朝向有利生长的因素靠近。这种对外界条件的反应被称作滑动反应(Taxis),又因具体的原因不同也有不同的名字,如趋化性,趋电性和趋光性,阿米巴黏菌的聚集很明显就是一种趋化性反应,同理还有负趋药性,生物会远离某些物质浓度高的地方,比如驱虫剂之于虫子。
总的来讲,阿米巴是朝着某种自我生产的诱饵物的浓度高的地方运动,聚集的,这鼓励我们围绕着一事实建立数学模型。最终目的是根据该性质建立一个创造一个跟该问题效果相近的简单模型。当然我们的建模都是在理论上的,且仅仅考虑了其中一个要素,在缺乏实验获得的参数支持和生物理论的情况下。并不能完全预测阿米巴的运动。
为了不让模型复杂化,我们在这个问题不考虑阿米巴与其捕食细菌的相互作用,有研究表明,即使在没有细菌的情况下阿米巴依然可以进行聚集,他们可以只由诱导物质和食物驱动,黏菌也可以完成聚集活动。
相同的目的,我们不考虑黏性的因素也会让我们的模型更清晰更方便理解,因为我们考虑的时期主要是在黏菌聚集完成前,这个时期阿米巴间很难产生黏性没有发生团聚,即使产生了黏性也是影响非常小的。
下面从不同的角度对化学战术运动进行建模,并建立经典的趋化方程。移动物种的化学战术运动建模可以从两个不同的角度进行:从微观或宏观角度[3],这两种方法都已经使用多年了,许多科学家都在研究这个课题。我们主要讨论的部分为宏观部分,辅以微观的观点加强理解[4]。
第2章 宏观角度
这里应该提出的第一种方法是宏观的观点,即把阿米巴群体视为一个整体,关注他们整体的流动聚集。这种方法导致了一个连续的反应扩散模型[5],其中阿米巴黏菌密度的扩散是用傅立叶和菲克定律建模的,反应被视为密度的函数,可能还有一些外部信号或控制物质[6]。
2.1一维阿米巴数学模型
我们认为阿米巴的聚集是由一种诱导物作用的,而这种诱导物又是由阿米巴黏菌自己分泌的,所以这就有一些有趣的现象
首先我们从简单的模型开始描述,因为阿米巴黏菌间的距离小于聚集中心之间的距离,因此我们采用连续介质模型,连续介质模型是流体力学中的一个重要模型,由欧拉在18世纪提出,通俗来讲就是假设流体内部的分子间没有间隙,完全占据所有其所属空间。这样我们可以把流体中的物理量都看作是时间和空间的连续函数,可以极大简化我们的模型。
假设整个聚集周期发生在一个平面上(x,y),再为了简单,我们假设各个物理量在y轴方向上没有,如此我们就只需要讨论x轴方向上的变化,即先考虑一维情况。
我们令表示在x处,t时刻的阿米巴黏菌浓度。然后我们需要考虑位于
区间上的黏菌,为任意数字,不是任意小的。
为此我们要为这个区间设计一个普遍的平衡定律,也就是将生物密度的变化由其区间内外净流动和区间内净生成描述,至于这个问题,的数量在区间中的净变化率等于穿过区域边界的的流量加上这个区间内的的净分裂数量,净产生数量。显然的流量是由边界上的流出量和流入量决定的,而的净产生数量则是由生成的数量和期间死亡的数量决定的。之所以称这个平衡定律是普遍的,是因为这个定律对很多物质的区域浓度都适用,很显然物质的增加是由内部生成和外界进入综合作用的效果,除此以外对大多数物质没有他法。
这样我们就把浓度问题分成了两部分,首先我们来计算通量密度J,这个量给出的是穿过边界=的净通过率,设定向的增加方向的阿米巴数量多于向的减少方向的则记通量密度J为正。
其次是区间内的的净生产率,,为生产数量减去死亡数量。
这样我们就能用公式表示出上面的平衡定律
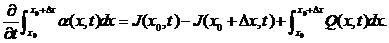
根据公式很容易联想到应用积分中值定理,可以把上公式转化为
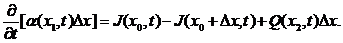 (2.1)
(2.1)
其中,,接着可以再在等式两边同时除以,然后取的极限,便可以得到阿米巴黏菌的微分形式的普遍平衡定律
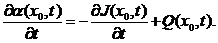 (2.2)
(2.2)
这里的可以是任意值。
备注1:
积分中值定理
设R为三维空间中具有体积V的一个连续封闭有界区域,0lt;Vlt;infin;,令f在R上连续,m和M分别表示f()在R上的极小值和极大值,那么在R中存在一个点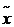 ,使得
,使得
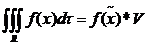 (2.3)
(2.3)
虽然上式是在三维空间中应用的,但仅需要稍作改变就恶意使其适用于m维空间中的n维联通有界闭区域(nlt;m)
由于阿米巴的生长发育过程较为复杂,不属于我们研究的主要内容,所以我们设定在聚集的过程中食物中断,因而不考虑再生的黏菌,又因为没有新生阿米巴,也能不考虑死亡的,综上在时间间隔内,我们可以设置
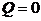
接下来我们将分情况讨论通量密度J的表达式。
2.1.1 无诱导物情况
首先我们考虑没有诱导物的情形,阿米巴的运动不受其他物质约束,在空间内做无规则运动,形成一种类似扩散的现象。
扩散现象(diffusion)是指物质从高浓度区域向低浓度区域转移直到均匀分布的一种现象,速率与物质的浓度梯度成正比,主要是由于物质密度差引起。那么就存在一种无规则流动量,驱使阿米巴从其阿米巴浓度高的地方在浓度低的区域,这样就可以确定一个事实,坐标处的通量大小直接取决于与邻近区域的浓度差。
可以用来表示邻近区域的浓度差,设
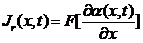 (2.5)
(2.5)
其中上式中的F为一未知函数,不过我们可以根据一些事实确定F的一些性质。阿米巴在无规运动时,向左运动的阿米巴数量和向右运动的应该是一样多的,在这种情形下,即为常数。故当为常数时,为0,
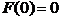 (2.6)
(2.6)
这样F的图像必须经原点,对F(s),如果s足够小,那么可以将函数图像近似为一条直线,设直线斜率为(其中,因为如果内外浓度差大于0,内部阿米巴则是净流出的),便可以得到一个简易的F表达式,
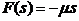
即
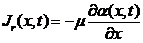 (2.7)
(2.7)
把式(2.2)(2.6)(2.7)结合,我们便可以得到
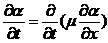 (2.8)
(2.8)
上式即为扩散方程,这类方程通常是来描述无规则运动粒子体系的浓度变化的,比如空气中的烟尘粒子的游动,常数决定了无规则运动的剧烈程度,术语为扩散率(diffusivity),也可以叫做游动性(motility)。
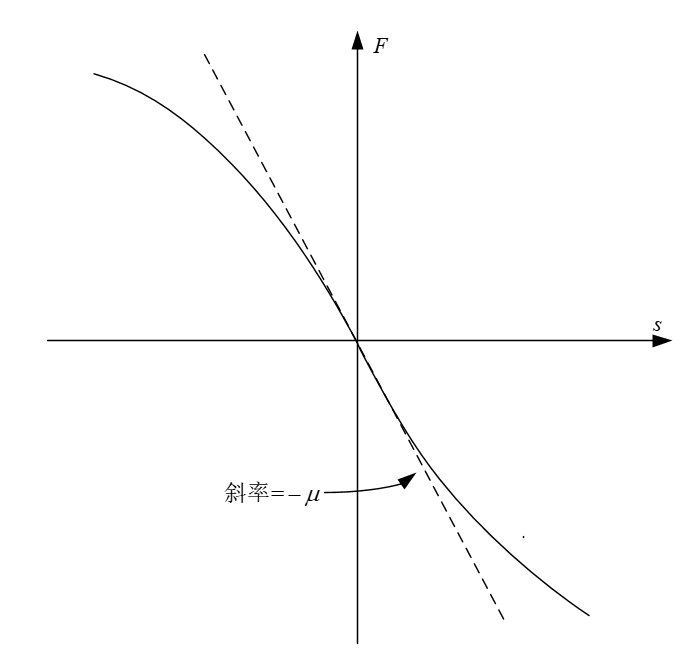
图2.1 函数F的一种可能曲线
2.1.2 存在诱导物情况
上面的结果是不存在诱导物的情况下获得的,现在需要考虑到阿米巴的趋药性,即由于化学物质浓度的变化引起生物的定向运动,所以在上一节节讨论的基础上,我们在(2.1)式加入一个,与加和,其代表了由于趋药性产生的阿米巴通量密度。
表示诱导物在x处,t时刻的浓度,同上一节的对阿米巴无规则运动的讨论,我们先假设也是诱导物梯度的函数,且在其值极小的情况下正比于
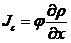 (2.9)
(2.9)
其中表示运动无规急剧程度,但对于,如果阿米巴的浓度增长到倍而诱导物密度不变,那么也会增长到倍,这说明了比例因子应当是阿米巴浓度的倍数(应该是的函数,倍数也是为了简化模型),这样我们获得
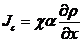 (2.10)
(2.10)
这里为趋药性强度的量度。与(2.7)不同,该式没有负号,这是因为阿米巴会朝着阿米巴少,而诱导物浓度高的地方运动。
这样(2.2)中的总通量密度就是无规运动作用部分和趋药性作用部分的结合,可以得到最终的阿米巴密度变化方程
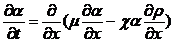 (2.11)
(2.11)
可以发现和,两个描述运动剧烈程度的量都有可能随着的变化而发生改变,但这里并不会影响我们分析建模的大致方向,只会在某些细节部分有些变化。
这里(2.11)式中会存在平方项,因为即使假设和无关于只是常数,(2.11)式中的项也会跟两个未知量和的乘积成正比,即为一个非线性项,这样以来对问题的数学分析就会变得更加复杂困难,不过这也是不可避免的情况。
(2.11)提供了未知量阿米巴密度的方程,其中还有未知量,下面我们还需要一个关于诱导物密度的方程,他的一般形式类似(2.2)式,同样是考虑通量和生成量,即:
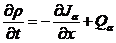 (2.12)
(2.12)
类似式(2.9),第一是边缘通量我们描述诱导物浓度的扩散通量还是由浓度对于x轴分布的微分确定的,即为:
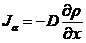 (2.13)
(2.13)
其次是生产率,前面我们假设的是在食物中断的情况没有黏菌的出生和死亡,但这里诱导物浓度受阿米巴数量影响的因为阿米巴会产生分泌物,所以净生产部分我们可以通过一个参数表示,,是单位黏菌密度的诱导物分泌率。
除了产生,诱导物也有“死亡”的概念,诱导物可能在一定条件下受物理或者化学影响失去活性(inactivation),从而独立于问题不再影响阿米巴分布。方便起见我们把衰减率和黏菌浓度取正比(黏菌过多可能干扰诱导物的反应)比例系数为k,新的为,
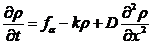 (2.14)
(2.14)
,k和D都取正常数。(2.11)和(2.14)分别给出了和两个未知函数的表示形式。
2.1.3 稳定性分析
阿米巴黏菌在耗尽食物供应后会突然开始积聚在一些非常有规则的聚集点上,如果驱动的压力增加的更大,光滑流过管道的流体会发展处强烈的随机漩涡,假设将少量的额外负荷加到一个金属结构上的话他就会坍塌,所有类似的或者相关的现象都可以看作平衡失稳(Balance instability)的例证。所谓平衡态,我们指的是问题的基本方程所允许的定常态,如果把一个系统置于稍许偏离平衡态的状态那么我们就可以说平衡态受到了扰动,扰动就是为了取得扰动状态我们强加给平衡体系的概念,如果在系统在延边的意义上,平衡态的初始扰动在变大那么我们可以说平衡态对扰动是不稳定的。这节讨论了当平衡的黏菌阿米巴体系由于自身或者条件的变化受到了部分扰动,整个体系的状态会如何变化[7]。
根据上节的工作我们可以获得方程(2.11)和(2.14)的一组精确解
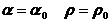 (2.15)
(2.15)
和 为常数,这里需要引入一个的概念,均匀态,一定区域内物质总量维持不动且各处分布均匀,密度相同,他也是一种平衡态。如果式(2.15)成立,我们称系统达到了均匀态,即当两者浓度都处于当前浓度,浓度不再随着时间的改变而变化。
备注:这里我们还需要有
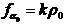 (2.16)
(2.16)
这也就是说在该均匀态时诱导物的分泌率和失活率是抵消的,维持了一定区域内的诱导物总量不变,单位面积内,保护了均匀态。
然而现实情况不会这么理想,就算阿米巴和诱导物的浓度达到了均匀态的条件,也会存在一些小的外界扰动影响均匀态,出现一些小波动,极可能破坏均匀态。
首先聚集开始是一个稳定的状态,整个黏菌体系处在均匀态,保持不变。后来可能由于某些参数的变化,或者黏菌开始局部聚集,系统开始稍稍偏离均匀态,我们要讨论的是这个微小的干扰会导致黏菌系统更加偏离平衡,还是会衰减,回归稳定。
接下来将要分析稳定性:




