椭圆曲线与某些特殊情况下Mordell-Weil群的计算毕业论文
2021-11-25 23:12:29
论文总字数:23366字
摘 要
本文阐述了椭圆曲线的基本概念和必要的算术性质, 回顾了任意数域 上的椭圆曲线的Mordell-Weil定理的证明框架与相关结论,在此基础上计算了某些特殊椭圆曲线的秩,讨论了某些特殊情形下的秩的约束行为,并且在最后阐述了什么是BSD猜想,所得的结果对于了解椭圆曲线的算术性质具有一定的意义。
上的椭圆曲线的Mordell-Weil定理的证明框架与相关结论,在此基础上计算了某些特殊椭圆曲线的秩,讨论了某些特殊情形下的秩的约束行为,并且在最后阐述了什么是BSD猜想,所得的结果对于了解椭圆曲线的算术性质具有一定的意义。
论文主要研究了某些情形下椭圆曲线的秩的精确计算和约束行为。
研究结果表明:在适当的假设下,利用Weil-偶对和上同调的工具证明了在基域上添加一个挠点时, 秩的上界被一个有限集合的元素个数所约束,同时利用该结论计算了一个较为复杂的例子。
本文的特色:体现了代数方法在数论对象上的一些初步应用。
关键词:椭圆曲线;Mordell-Weil群;秩的计算
Abstract
This paper expounds the basic concepts and necessary arithmetic properties of elliptic curves, reviews the proof framework and related conclusions of the Mordell-Weil theorem for elliptic curves in arbitrary number fields, and on this basis, calculates the ranks of some special elliptic curves in some special cases, the rank constraint behavior, and at the end elaborated on what is the BSD conjecture, the results obtained have some significance for understanding the arithmetic properties of elliptic curves.
The thesis mainly studies the precise calculation and constraint behavior of the elliptic curve rank in some cases..
The results of the study show that: under appropriate assumptions, using the tools of Weil- pairing and cohomology prove that when a torsion point is added to the base field, the upper bound of the rank is constrained by the number of elements in a finite set, and using the conclusion , a more complicated example is calculated.
The characteristics of this article: it embodies some preliminary applications of algebraic methods on the objects of number theory.
Key Words:elliptic curve; Mordell-Weil group; rank calculation
目 录
第1章 绪论 1
1.1 研究背景及意义 1
1.2 研究内容及主要方法 2
第2章 椭圆曲线的基本概念与性质 4
2.1 Weierstrass方程与群律 4
2.2 除子与同源映射 6
2.3 形式群 7
2.4 局部域上的椭圆曲线 8
第3章 Mordell-Weil定理 11
3.1 弱Mordell-Weil定理 11
3.2 高度函数 13
第4章 Mordell-Weil群的计算 19
4.1 挠点的计算 19
4.2  上的含有一个2阶有理点的情形 19
上的含有一个2阶有理点的情形 19
4.3 Weil-偶对 22
4.4 连接同态 与
与 23
23
4.5 特殊情形下估计秩上界的一种方式 24
4.6 曲线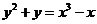 27
27
第5章 什么是BSD猜想 31
5.1 整体极小Weierstrass方程 31
5.2 不变微分 32
5.3 典范高度与椭圆正则子 33
5.4 Shafarevich-Tate群 35
5.5  -级数 36
-级数 36
第6章 总结 39
参考文献 40
致 谢 42
绪论
1.1 研究背景及意义
我们知道多项式方程定义了一条曲线 , 我们总假设曲线是非奇异的, 当该多项式的系数都是有理数时, 我们可以求其有理解, 即
, 我们总假设曲线是非奇异的, 当该多项式的系数都是有理数时, 我们可以求其有理解, 即 均是有理数的解, 我们把全体有理解的集合记作
均是有理数的解, 我们把全体有理解的集合记作 . 这类方程的有理解求解问题一直是数论的核心问题之一. 曲线
. 这类方程的有理解求解问题一直是数论的核心问题之一. 曲线 有一个重要的不变量即亏格, 现在我们知道
有一个重要的不变量即亏格, 现在我们知道 是一次和二次多项式的时候曲线具有亏格
是一次和二次多项式的时候曲线具有亏格 , 在四次及以上的情形具有亏格
, 在四次及以上的情形具有亏格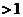 , 而关于亏格
, 而关于亏格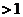 的曲线, 有如下定理:
的曲线, 有如下定理:
定理1.1.1.[Faltings,1983] 如果非奇异曲线的亏格 , 那么
, 那么 有限.
有限.
在亏格为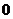 的情形, 关于
的情形, 关于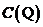 也有了成熟的结果, 一次的情形很简单, 对于有理数域上的二次曲线, 如果它具有一个有理点, 那么这条曲线上必有无穷多个有理点, 且我们可以求出全部的有理点(方法见[1]). 在亏格等于
也有了成熟的结果, 一次的情形很简单, 对于有理数域上的二次曲线, 如果它具有一个有理点, 那么这条曲线上必有无穷多个有理点, 且我们可以求出全部的有理点(方法见[1]). 在亏格等于 时, 情况极其复杂, 我们把多项式方程
时, 情况极其复杂, 我们把多项式方程 定义的亏格为
定义的亏格为 的非奇异曲线称为椭圆曲线, 并取记号
的非奇异曲线称为椭圆曲线, 并取记号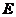 . 这也是我们将要讨论的对象, 此时在仿射平面上
. 这也是我们将要讨论的对象, 此时在仿射平面上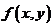 可以写成三次方程的形式. 人们已经知道定义在
可以写成三次方程的形式. 人们已经知道定义在 上的椭圆曲线上的有理点
上的椭圆曲线上的有理点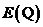 构成一个交换群(见[2][3]). 在1922年,Mordell首先证明了
构成一个交换群(见[2][3]). 在1922年,Mordell首先证明了 是有限生成的阿贝尔群(见[4])(称为Mordell-Weil群), 该结论被称为Mordell-Weil定理, 该定理是BSD猜想的前提条件(见[5]), 也是我们将要讨论的主要定理, 不过我们会在任意数域
是有限生成的阿贝尔群(见[4])(称为Mordell-Weil群), 该结论被称为Mordell-Weil定理, 该定理是BSD猜想的前提条件(见[5]), 也是我们将要讨论的主要定理, 不过我们会在任意数域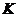 上来讨论. 有限生成阿贝尔群的结构定理告诉我们椭圆曲线上有理点所具有的统一形式:
上来讨论. 有限生成阿贝尔群的结构定理告诉我们椭圆曲线上有理点所具有的统一形式:

这里的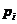 是素数, 不必各不相同. 但如何计算它在一般情况下仍然是一个悬而未决的问题, 计算的关键是计算数值
是素数, 不必各不相同. 但如何计算它在一般情况下仍然是一个悬而未决的问题, 计算的关键是计算数值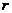 ,它被称为椭圆曲线的秩, 美国Clay数学研究所所举世界七大数学难题之一的BSD猜想就是试图解释椭圆曲线的秩
,它被称为椭圆曲线的秩, 美国Clay数学研究所所举世界七大数学难题之一的BSD猜想就是试图解释椭圆曲线的秩 与一类叫做
与一类叫做 函数的对象
函数的对象 在
在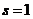 处零点阶数之间的关系, 它断言可以通过
处零点阶数之间的关系, 它断言可以通过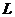 函数的性质来判定椭圆曲线上是否具有无限多个有理点, 虽然BSD猜想至今并没有被解决,但是数学家们仍然取得了部分结果, 例如:
函数的性质来判定椭圆曲线上是否具有无限多个有理点, 虽然BSD猜想至今并没有被解决,但是数学家们仍然取得了部分结果, 例如:
定理1.2.(见[5]) 若 , 其中
, 其中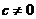 , 那么
, 那么 或者
或者 时, BSD猜想成立.
时, BSD猜想成立.
本文也将研究椭圆曲线的秩的问题, 对某些特殊椭圆曲线计算其Mordell-Weil群.
请支付后下载全文,论文总字数:23366字




