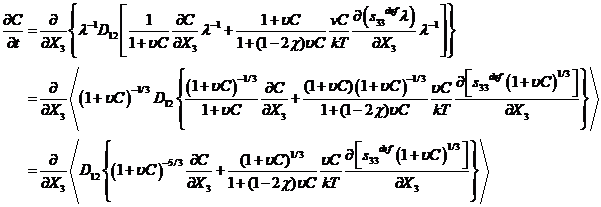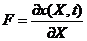非Fickian型溶剂扩散与凝胶溶胀大变形的耦合行为研究毕业论文
2020-02-18 09:58:58
摘 要
凝胶的溶胀是一个耦合了凝胶网络大变形和溶剂分子扩散的过程,其溶胀变形规律与高分子网络中的溶剂扩散特性有着密切的联系。目前,对溶胀凝胶内Fickian扩散的理论研究已经较为成熟。然而在许多玻璃态高聚物与有机溶剂的材料体系中,溶剂分子的扩散不再遵循经典的Fick定律,而是表现出非Fickian型扩散的运移特性,现阶段人们对这方面的认识并不充分,相关研究大多还处于宏观实验观测的水平,对于耦合凝胶溶胀大变形及其内部非Fickian扩散的理论研究无疑有待补充和完善。
本文致力于在凝胶溶胀行为耦合分析框架下,考虑处于受力平衡和溶剂平衡状态下的凝胶的溶胀过程,并引入标准线性黏弹性本构关系,对传统Fick定律进行一定修正,从而建立一个能描述凝胶材料内部网络松弛和溶剂分子非Fickian流动扩散的理论模型。利用该溶胀体系的控制方程,结合适当的边界条件进行求解,得到反映溶胀凝胶内部溶剂分子浓度变化的结果,并将之与现有实验结果作对比分析。本文的主要成果体现在以下两点:
(1)基于连续介质力学及非平衡热力学理论,建立了一套能够表征凝胶溶胀变形和非Fickian扩散耦合行为的控制方程,包括凝胶的黏弹性本构方程、平衡条件、溶剂扩散方程、分子守恒方程等。
(2)基于导出的控制方程,针对一维细长柱状PEG-DA凝胶棒与水溶剂的接触、水溶剂在其内部的扩散,以及试样的溶胀大变形耦合过程进行求解,并将得到的数值解与现有实验数据进行对比分析,以此结果为例,总结了Fickian扩散与非Fickian扩散的差异性。
关键词:凝胶;非Fickian扩散;溶胀;大变形;黏弹性
Abstract
The swelling of gel is a process that couples the large deformation of the polymer network with the diffusion of solvent molecules. The swelling deformation rule has much to do with the diffusional law in the cross-linked polymer network. At present, the theory of the Fickian diffusion in the swollen gel has been developed maturely. However, the studies of the non-Fickian diffusion are mostly experiments on the relatively macroscopic level. Thus, it is necessary to do much more work to fully develop the coupled theory of the large deformation and non-Fickian diffusion in the polymeric gel.
This paper is devoted to formulate a set of equations which is able to model the swelling and the non-Fickian diffusion in the polymeric gel, based on the framework of the coupled theory, considering the gel in equilibrium with an external solvent and mechanical load, as well as modifying the traditional Fick’s law. By means of solving these controlling equations numerically under particular initial-boundary value conditions and comparing them with some present experimental results, main results of this paper are as follows:
(1)Based on continuum mechanics and thermodynamics, this paper formulates a set of controlling equations which described the swelling of gel and the non-Fickian diffusion in the gel. These equations include the viscoelastic constitutive equation of the gel, the equilibrium condition, the diffusion equation, as well as the mass conservation equation, etc.
(2)By solving these controlling equations in case of one-dimensional cylindrical gel, and comparing their numerical results with some experimental data, this paper specifically analyzes the differences between Fickian and non-Fickian diffusion.
Key Words: Non-Fickian diffusion; Gel; Swelling; Large deformation; Viscoelasticity
目 录
第1章 绪论 1
1.1 研究背景及目的意义 1
1.2 研究历史与现状 2
1.3 研究内容与技术路线 3
1.3.1 研究内容 3
1.3.2 技术路线 4
1.4本文工作 4
第2章 建立凝胶溶胀系统理论模型 6
2.1 力学模型的建立 6
2.2 系统状态方程的导出 7
2.2.1 力平衡方程 7
2.2.2 分子不可压缩条件 8
2.2.3 修正后的状态方程 8
2.3 非Fickian型扩散与凝胶溶胀大变形的控制方程 9
2.3.1 溶剂化学势的具体形式 9
2.3.2 非Fickian扩散定律 10
2.3.3 溶剂分子的质量守恒方程 12
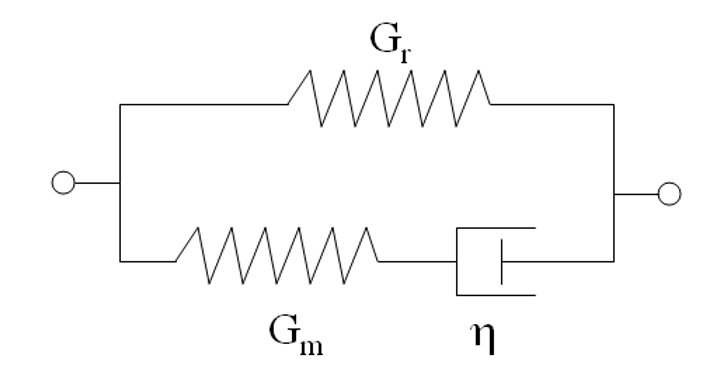
2.4 凝胶材料的黏弹性本构模型 13
2.5 本章小结 15
第3章 一维柱状凝胶棒的溶胀变形分析 16
3.1 柱状凝胶棒的理论模型 16
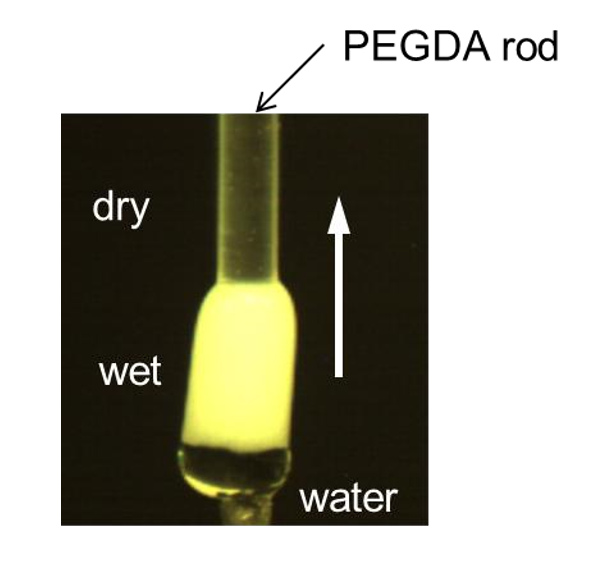
3.1.1 本构和扩散方程的具体形式 16
3.1.2 边界条件的设定 18
3.1.3 尺度化的探讨 20
3.2 实验对比分析 21
3.2.1 相关参数的确定 21
3.2.2 结果对比与讨论 22
3.3 本章小结 24
第4章 结论与展望 26
4.1 全文总结 26
4.2 工作展望 26
参考文献 27
致 谢 29
第1章 绪论
1.1 研究背景及目的意义
凝胶材料是一种由长链聚合物相互交联而成的三维网络吸收大量溶剂分子,从而发生溶胀而形成的高分子聚合物。在一定条件下,该类材料可以大量吸收与释放溶剂分子,从而发生可逆的大变形。由于引起凝胶变形的原因有两种:一种是长链聚合物间存在的弹性形变;另一种是长链聚合物与溶剂分子间存在的粘性迁移,因此凝胶材料同时具有固体和液体的性质,故而其常被广泛应用于药物释放[1]、组织工程[2]、传感器件[3]、化学膜[4]等各领域。为了能够充分利用凝胶材料的这种结合特性,有必要着重关注凝胶材料或其制品的制造与设计的过程中,与溶胀变形相关的力学问题,并对材料溶胀变形与凝胶内溶剂分子扩散的耦合过程做一定的分析,发展能够准确描述该耦合过程的理论模型。
凝胶的溶胀是一个发生大变形的过程。一方面,溶胀的变形规律与溶剂分子在高分子网络内的扩散规律有很大关系。凝胶内溶剂分子的扩散行为一般分为两类:一类是Fickian扩散(Fickian diffusion);另一类是非Fickian扩散(Non-Fickian diffusion),又称二型扩散(Case Ⅱ diffusion)。凝胶内溶剂分子的Fickian扩散行为可以由经典的Fick定律来描述:Fick第一定律指出,溶剂的扩散通量将于凝胶内溶剂浓度的梯度成一种线性关系;Fick第二定律则描述了凝胶内溶剂分子的守恒关系。另一方面,溶剂分子在高分子聚合物中的扩散类型也与高分子聚合物自身处于橡胶态还是玻璃态密切相关。随着对各类高分子聚合物中溶剂分子扩散过程研究的深入,人们发现,对于玻璃态聚合物,当其所处的环境温度接近或低于聚合物本身的玻璃态转变温度时,聚合物内的溶剂分子的扩散行为将呈现为非Fickian扩散类型,而这种扩散现象无法用传统的Fick定律进行描述,故而寻求非Fickian扩散现象的描述方程是很有必要的。
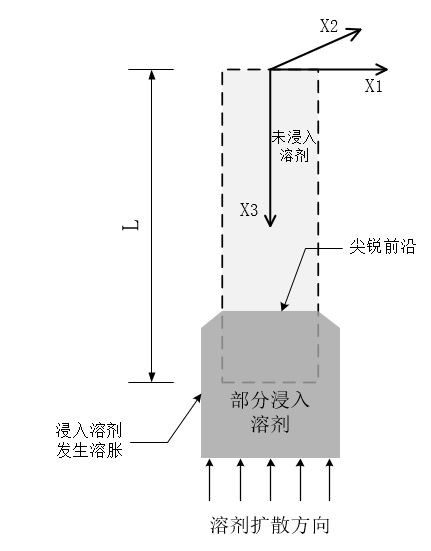
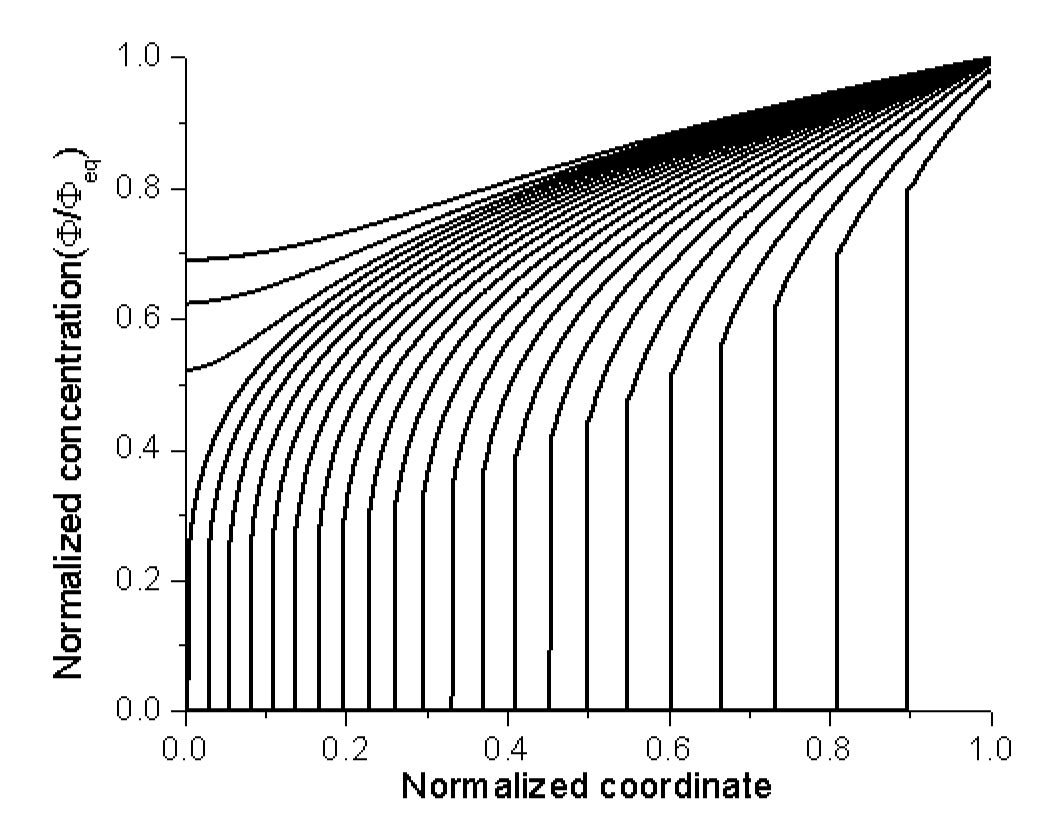
现有试验结果表明[5],凝胶内的非Fickian扩散现象主要具有以下几个显著的特点:(1)聚合物的溶胀部分和未溶胀部分之间存在一个尖锐的溶剂扩散分界面,也叫尖锐前沿;(2)对于没有完全浸没在溶剂中的聚合物而言,其溶胀部分呈现橡胶态,而未溶胀部分仍呈玻璃态,并且前者内溶剂分子扩散系数的数量级远大于后者(见图1.1);(3)溶剂分子在聚合物内的扩散速率,也即尖锐分界面的移动速率近似为一个常数,并且在此过程中经常伴随有松弛效应等黏弹性材料特性的出现[5]。目前,无论是理论方面,还是实验方面,人们对凝胶内Fickian扩散过程的认识已经较为充实。然而,相比于传统Fickian扩散,人们对凝胶内非Fickian扩散行为的认识则一般停留于实验的宏观层面[7]-[9],缺乏对其深层机理的系统性理论分析。因此有必要开展进一步的理论工作,对这部分内容加以完善补充。
本文致力于为凝胶溶胀变形与溶剂分子非Fickian扩散的耦合效应建立一种一般理论模型。具体方法则是将凝胶材料作为黏弹性材料进行变形分析,采用一种线性黏弹性本构模型,同时对经典Fick定律做合理修正,用以描述溶剂分子在凝胶内的非Fickian扩散过程,最后得到一组凝胶溶胀体系的控制方程,并对这组方程进行求解,以获得凝胶内溶剂分子浓度的变化与分布情况。本文最后还在一定的边界条件下,对相关特殊模型进行了求解,并将获得的数值结果与现有实验结果作了一定的对比分析。
(a)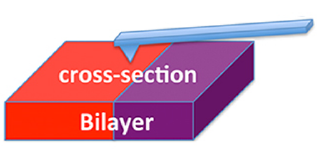 (b)
(b)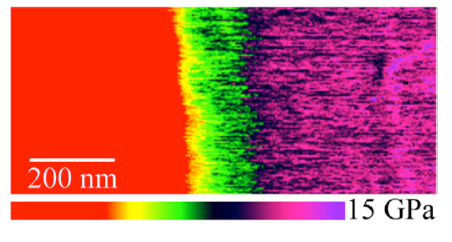
图1.1 聚合物溶胀过程中的非Fickian扩散现象[5]:(a)使用扫描探针测定试样表面的模量(b)测定的模量分布图,由此可见玻璃态与橡胶态区域间的尖锐分界面
1.2 研究历史与现状
早在1966年,Alfrey[10]等人就在玻璃态聚合物内观察到一种不同于普通扩散的异常扩散现象,并将这种不遵循经典Fick定律的扩散行为命名为非Fickian扩散。不同于传统Fickian扩散类型,在非Fickian扩散中,搭载溶剂分子的溶胀凝胶将以一种尖锐前沿的形式,保持近乎一定的速率向未溶胀部分的玻璃态聚合物中移动。非Fickian现象一经发现,便引起了诸多学者的密切关注。多年来,无论是在其现象学方面还是动力学方面,各学者分别基于不同的物理图像和假设,相继提出各种复杂程度的理论模型[11]。
Thomas和Windle[14]提出了一种非Fickian扩散过程主要机制的解释,即认为该类扩散是由聚合物内及与其接触的环境溶剂分子化学势或浓度差异驱动的。他们还指出,在非Fickian扩散中,凝胶内部溶剂分子的扩散速率至少要高于凝胶高分子网络结构松弛速率的量级,此时经典的Fick定律不再适用,凝胶材料应被作为一种黏弹性材料进行考虑。在非Fickian扩散中,溶剂分子的扩散行为将受聚合物内的黏弹变形响应控制,高分子聚合物的黏弹变形与溶剂分子的扩散过程需要被同时考虑。基于此,Thomas和Windle建立了一套关于凝胶内非Fickian扩散与溶胀变形的理论模型。当然必须指出的是,作为这方面初步探索的结果,TW模型的理论框架尚无法完全准确、定量的描述溶剂分子扩散的动力学行为,但他们的工作吸引了更多学者致力于对非Fickian扩散的实验观测[15]-[17],而这些实验结果在一定程度上也验证了该理论模型的合理性。与此同时,大量的非Fickian扩散观测实验也促进了各学者对此类非常规扩散现象的理论研究[18]-[19]。
Wu和Peppas[20]在TW模型的基础上做了一些改进。他们的工作则是重点关注了与控制非Fickian扩散过程息息相关的两个动力学过程:一是高分子聚合物网络的松弛过程,二是溶剂分子的扩散过程。这两个过程耗时的相对长短将由一个Deborah数来表征,大的Deborah数则意味着整个扩散过程将由网络的松弛过程控制;相应地,小Deborah数则意味着扩散过程将由溶剂分子的扩散过程控制主导。本构关系方面则采用了Maxwell黏壶来表征凝胶材料的线性黏弹性。
Argon等人[21]提出了一种玻璃态聚合物吸收溶剂分子的非Fickian扩散理论模型。该理论模型清楚地区分了由于化学势差异诱导的驱动力与材料位错引起的阻碍溶剂分子渗透的压力。Liu等人[22]则是通过引用一个能够将应力、浓度和时间联系起来的合适函数,具体分析了溶剂分子渗透进凝胶内部的非Fickian扩散过程,从而得到了平衡状态下,溶胀凝胶内部的应力分布情况。
Ferreria等人[23]的文章中提到,由于溶剂分子扩散会引起一种可以产生阻碍流体分子布朗运动的应力的变形,因此越来越多的学者倾向于在扩散模型方面采用一种修正的扩散通量形式,该形式将同时计及Fickian扩散通量与非Fickian扩散通量。在该文中,关于非Fickian扩散通量方面,则采用达西定律和哈根-泊肃叶方程两种方法得到扩散速率,材料本构方面则采用了马克斯威尔-维谢尔模型的非线性黏弹本构关系。
El Aissaoui等人[24]建立了一个关于溶剂分子在溶胀的黏弹性凝胶无孔膜中的非Fickian型扩散行为的理论模型。该模型采用连续介质力学和非平衡热力学方法,明确耦合了变形和扩散两种过程,并给出了一系列时间演化方程,用于求解凝胶内溶剂浓度、非Fickian扩散通量及凝胶内应力的分布情况。
总之,非Fickian扩散与凝胶溶胀变形的耦合效应,主要表现为高分子网络松弛速率与溶剂分子扩散速率的一种竞争机制[14]。要准确描述凝胶溶胀过程中大变形和非Fickian扩散的耦合行为,必须合理考虑凝胶材料的黏超弹性,并寻求适用于非Fickian扩散规律的扩散方程。
1.3研究内容与技术路线
1.3.1 研究内容
本研究以新型高分子凝胶为研究对象,针对凝胶内溶剂分子非Fickian扩散与凝胶黏超弹性大变形耦合行为,开展一定的基础研究。具体内容如下:
(1)建立凝胶大变形与溶剂分子非Fickian扩散耦合行为的理论模型
基于连续介质力学理论,推导统一描述高分子聚合物凝胶力学变形与化学溶胀耦合 行为的控制方程,包括凝胶材料的黏弹性本构方程、溶剂分子的质量守恒方程、遵循非Fickian定律的扩散方程和平衡条件等。通过求解控制方程得到凝胶内溶剂分子的浓度变化和分布情况。
(2)结合初边值条件求解控制方程并与现有实验结果作比对分析
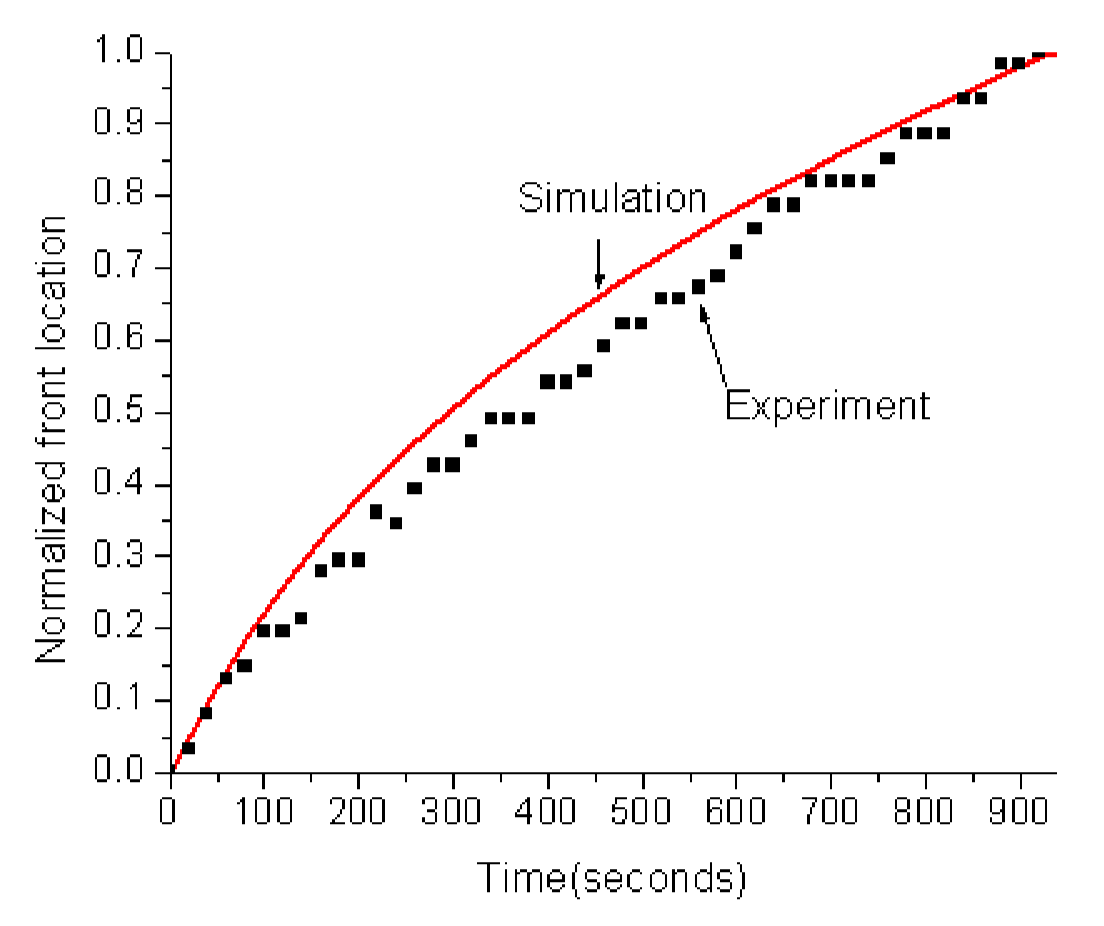
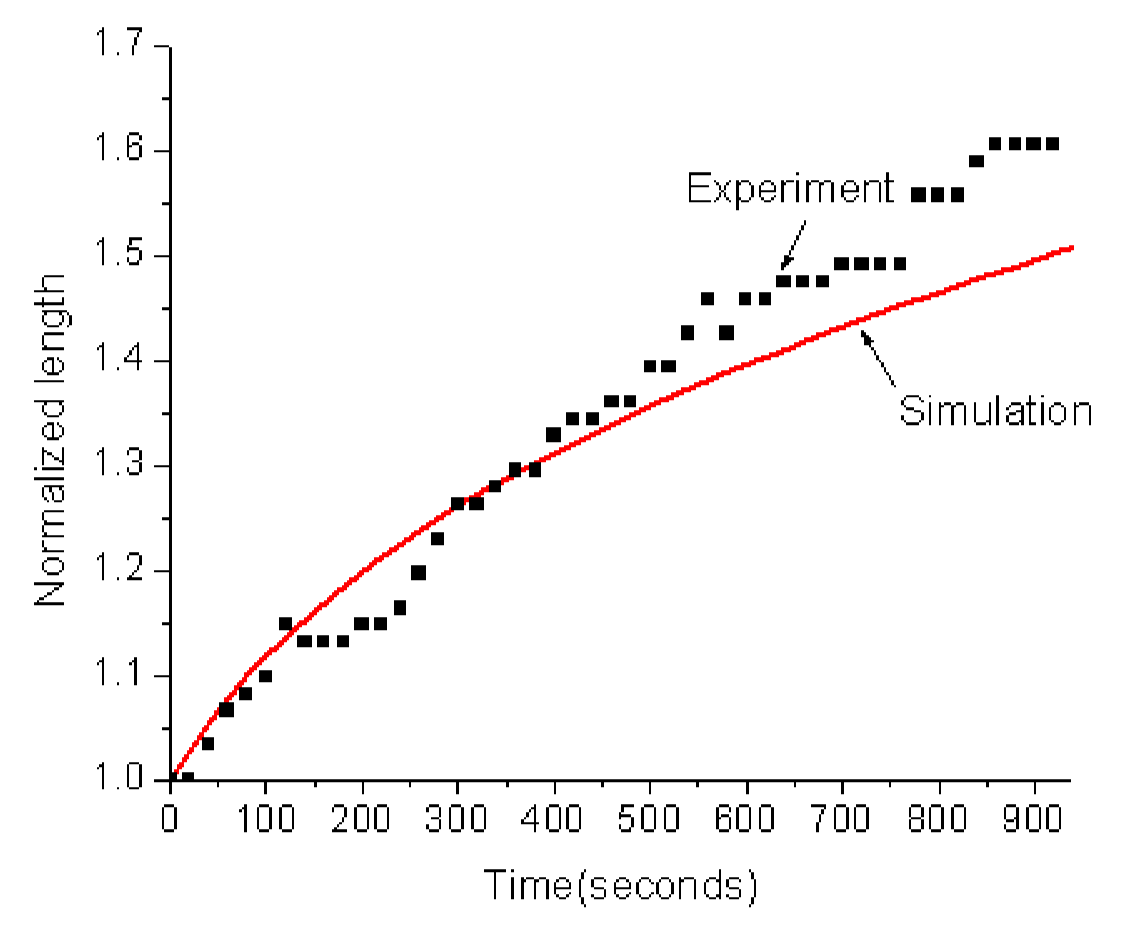
基于理论推导结果,结合具体算例,在无约束情况(即自由边界条件)下,讨论柱型凝胶溶胀模型,并合理简化关于溶剂浓度的偏微分方程,获得溶剂浓度函数的变化规律,再将求解的结果与现有实验结果进行对比分析,得出相应结论。
1.3.2 技术路线
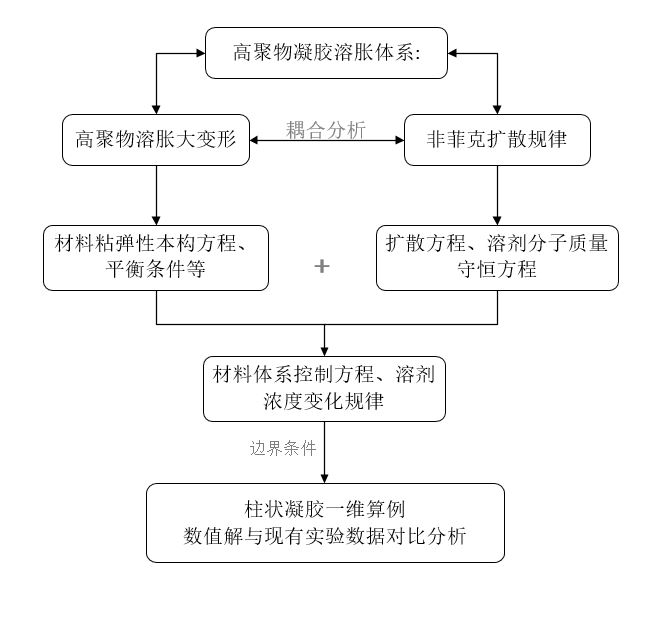 根据上述研究思路,本文拟采用的技术路线如图1.2所示。总体思路即以凝胶溶胀材料体系为研究对象,针对凝胶内溶剂分子非Fickian扩散行为,将凝胶溶胀大变形与溶剂扩散耦合起来,进行理论模型的建立与求解。
根据上述研究思路,本文拟采用的技术路线如图1.2所示。总体思路即以凝胶溶胀材料体系为研究对象,针对凝胶内溶剂分子非Fickian扩散行为,将凝胶溶胀大变形与溶剂扩散耦合起来,进行理论模型的建立与求解。
图1.2 技术路线图
1.4本文工作
针对凝胶材料吸收大量溶剂分子发生溶胀大变形,及其与凝胶内溶剂分子非Fickian扩散过程的耦合行为,本文拟对这种耦合过程的微观理论机理展开研究。该研究能够加深对凝胶溶胀与二型扩散相关机理的认识,对凝胶材料及其制品的制作与设计有一定的参考意义。
本文共分为四章。
第一章 绪论。概括介绍凝胶溶胀变形及其内部溶剂非Fickian扩散特点;简要介绍国内外相关研究现状;总结本文研究内容与目的,并提出技术路线。
第二章 凝胶溶胀系统理论模型的建立。基于连续介质力学理论与非平衡热力学理论,推导考虑了分子不可压缩条件情况下的凝胶溶胀变形的力平衡修正方程,并给出现时构型与参考构型之间的转换关系;在经典Fick扩散定律的基础上做一定修正,提出表征溶剂分子非Fickian扩散的扩散方程,同时给出系统的质量守恒方程;基于标准线性黏弹性本构关系及前人提出的描述系统状态的自由能密度函数,采用类比的思想,得到考虑凝胶材料黏弹性的大变形黏弹性本构方程,为凝胶溶胀大变形时凝胶内部黏弹应力与应变定量关系提供依据。
第三章 一维柱状凝胶棒的溶胀变形分析。针对第二章中建立的扩散方程、质量守恒方程以及凝胶材料黏弹性本构关系,在一维柱状凝胶棒的自由溶胀态下进行分析,考虑简化条件,得到柱状凝胶试样的对应控制方程,再结合具体的边界条件,运用数值分析软件对方程进行求解,并将求解结果与现有实验数据进行对比分析。
第四章 总结与展望。
第2章 建立凝胶溶胀系统理论模型
2.1 力学模型的建立
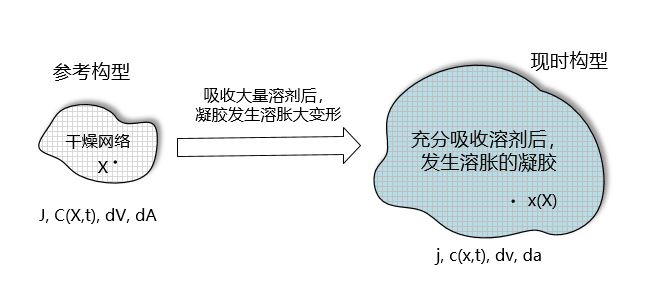
凝胶材料是一种由三维高分子网络及其内部的溶剂分子组成的高分子聚合物。如图2.1所示,当吸收大量溶剂分子时,凝胶材料会发生溶胀大变形。
|
图2.1 凝胶溶胀变形示意图 |
本文选取不受外部荷载的干燥聚合物网络作为参考状态。将网络中的每个小单元以其自身在参考状态下的材料坐标X标记。当聚合物网络发生变形时,网络中坐标为X的小单元将移动到坐标为x(X,t)的位置。那么,在时间t的当前状态下,可以将变形梯度定义为:
| (2.1) |
设定凝胶内溶剂分子的化学势为μ(X,t),单个溶剂分子的体积为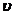 。在参考状态下,单位体积凝胶材料内的溶剂分子数量占比为C(X, t),若选取体积元为dV,其中包含的溶剂分子数目即为C(X, t) dV;若单位时间内通过单位面积的溶剂分子数目为J(X, t),选取面积元为dA(法向单位矢量为N),则单位时间通过该面积元的溶剂分子数量为
。在参考状态下,单位体积凝胶材料内的溶剂分子数量占比为C(X, t),若选取体积元为dV,其中包含的溶剂分子数目即为C(X, t) dV;若单位时间内通过单位面积的溶剂分子数目为J(X, t),选取面积元为dA(法向单位矢量为N),则单位时间通过该面积元的溶剂分子数量为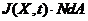 。相应的,在现时构型中,单位体积凝胶材料内的溶剂分子数量占比为c(x, t),选取体积元为dv,其中包含的溶剂分子数目即为c(x, t)dv;类似可定义流动矢量j、面积元da(法向单位矢量为n)和单位时间内通过该面积元的溶剂分子数量
。相应的,在现时构型中,单位体积凝胶材料内的溶剂分子数量占比为c(x, t),选取体积元为dv,其中包含的溶剂分子数目即为c(x, t)dv;类似可定义流动矢量j、面积元da(法向单位矢量为n)和单位时间内通过该面积元的溶剂分子数量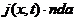 。
。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: