摘 要

滚动轴承是旋转机械中经常发生故障的部件,其工作状态影响着整个旋转机械的运行状态，所以对其进行诊断就尤为重要。滚动轴承故障诊断主要包括采集振动信号、特征提取、模式分类三部分，其中特征提取是最关键的环节。滚动轴承的故障信号，往往具有高维，非线性，非高斯分布等特征。拉普拉斯特征映射算法(Laplacian Eigenmaps ,LE)是一种聚类性较好的流形学习算法，且具有处理高维非线性数据的能力，所以将LE算法应用于滚动轴承故障诊断，并在MATLAB平台上进行一些比较实验来验证其有效性。

以滚动轴承作为研究对象，将LE算法应用于滚动轴承的故障状态识别，建立基于LE的滚动轴承故障状态识别模型。该模型利用LE算法，直接从原始振动信号构建的高维数据空间中，提取出低维流形特征，并将其输入K近邻分类器中进行分类。为了进一步验证LE算法的有效性，将LE算法与核主成分分析算法（KPCA）、核判别分析算法（KDA）进行对比试验。主要有以下四组试验：四种故障类型识别、五种故障损伤程度识别、不同负载下故障的识别、七种随机故障的识别。在这几组实验中，LE算法始终表现出了良好的聚类性以及较高的故障识别准确率，充分验证了LE算法对于滚动轴承故障识别的有效性。最后，研究了LE算法的特征维数和近邻点个数对滚动轴承故障识别精度的影响。

关键词：滚动轴承；故障诊断；特征提取；拉普拉斯特征映射

Abstract

Rolling bearing is a component which often breaks down in rotating machinery, and its working state affects the running state of the whole rotating machinery.So it is very important to diagnose it. Fault diagnosis mainly includes three parts, such as collecting vibration signal, feature extraction and pattern classification, among which feature extraction is the most critical link. The fault signal of rolling bearing often has the characteristics of high dimensional, nonlinear, non-Gaussian distribution and so on. Laplace feature mapping algorithm (Laplacian Eigenmaps, LE) is a well-clustering manifold learning algorithm with the ability to handle high-dimensional nonlinear data, so the LE algorithm is applied to the fault diagnosis of rolling bearings, and some comparative experiments are carried out on the MATLAB platform to verify its effectiveness. Taking rolling bearings as the research object, the LE algorithm is applied to the fault state identification of rolling bearings, and the fault state identification model of rolling bearing based on LE is established. Using LE algorithm, the model extracts the low dimensional manifold features directly from the high-dimensional data space constructed by the original vibration signal, and classifies them into the K neighbor classifier. In order to further verify the validity of LE algorithm, the LE algorithm is compared with the kernel principal component analysis algorithm (KPCA) and the kernel discriminant analysis algorithm (KDA). There are four groups of tests: four fault type identification, five fault damage degree identification, fault identification under different loads, and identification of seven kinds of random faults. In these groups of experiments, LE algorithm always shows good clustering and high fault recognition accuracy, and fully verifies the effectiveness of LE algorithm for the fault identification of rolling bearings. Finally, the influence of the characteristic dimension and the number of near-neighbor points of LE algorithm on the fault recognition accuracy of rolling bearing is studied.

Key Words：Rolling bearing ; Fault diagnosis ; Feature extraction ; Laplacian Eigenmap

目 录

摘 要 I

Abstract II

第1章 绪论 1

1.1 研究目的及意义 1

1.2滚动轴承故障诊断技术的研究现状状 1

1.3流形学习与拉普拉斯特征映射在机械故障诊断领域的研究现状 2

1.4研究(设计)的基本内容、目标、拟采用的技术方案及措施 3

第二章 拉普拉斯特征映射算法及基于该算法的智能诊断模型 4

2.1流形学习方法与分类介绍 4

2. 2 LE 算法基本原理 5

2.3其它几种流形学习算法 6

2.3.1核主成分分析算法 6

2.3.2核判别分析算法 7

2.4基于LE算法的故障诊断模型 8

第三章 故障状态识别实验 9

3.1实验装置 9

3.2三种诊断方法实验分析 10

3.2.1 实验方案设计 10

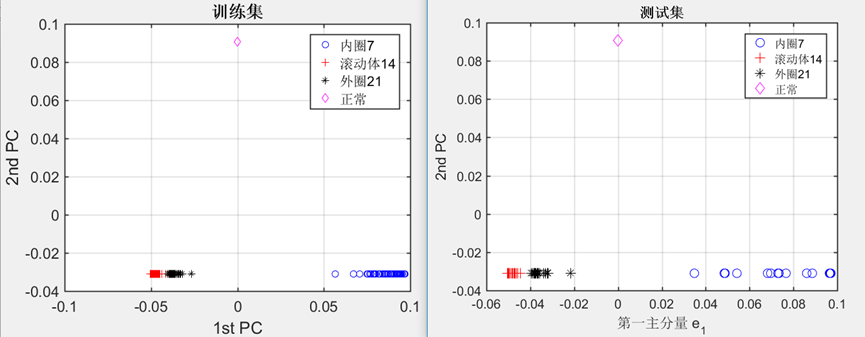
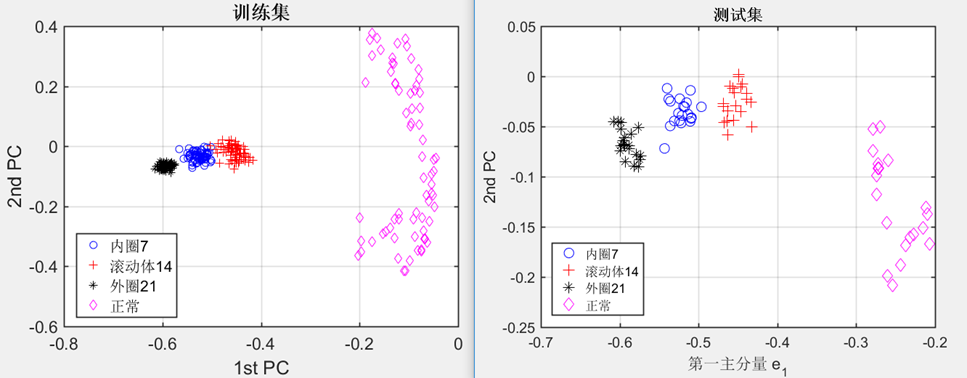
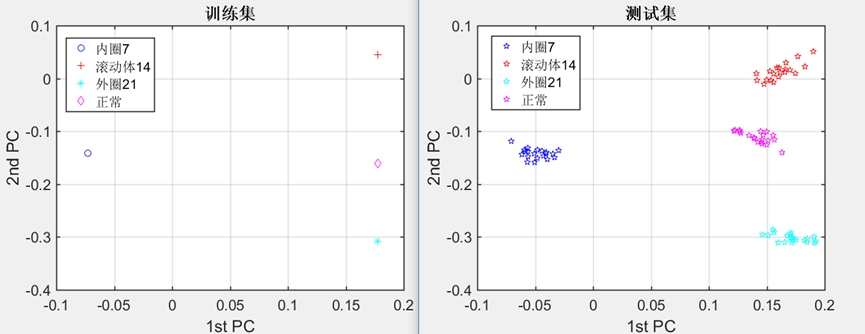
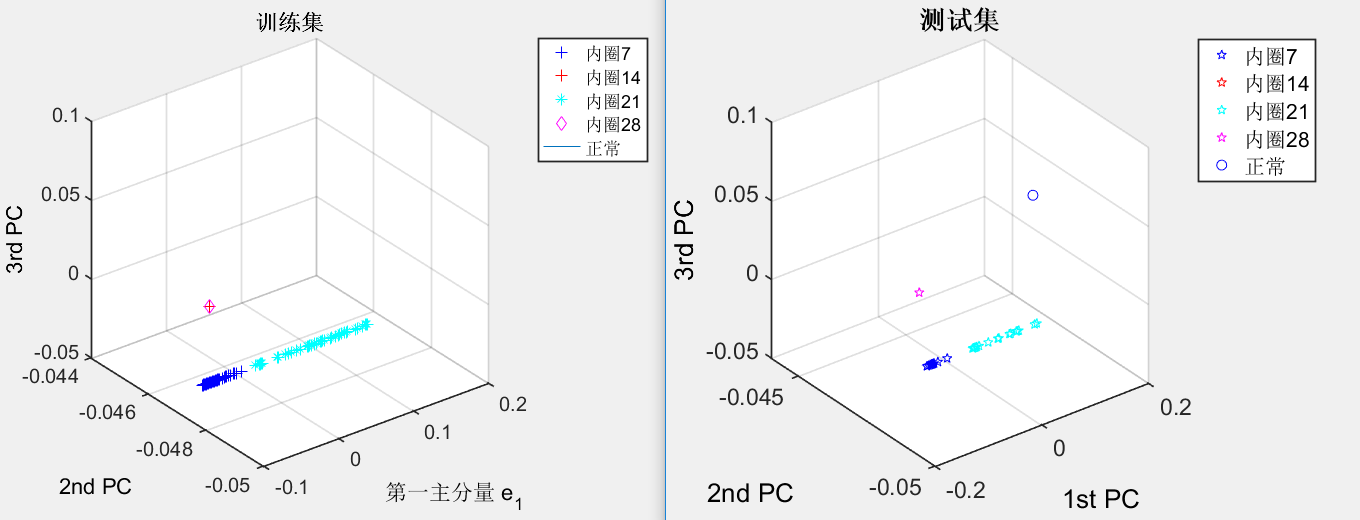
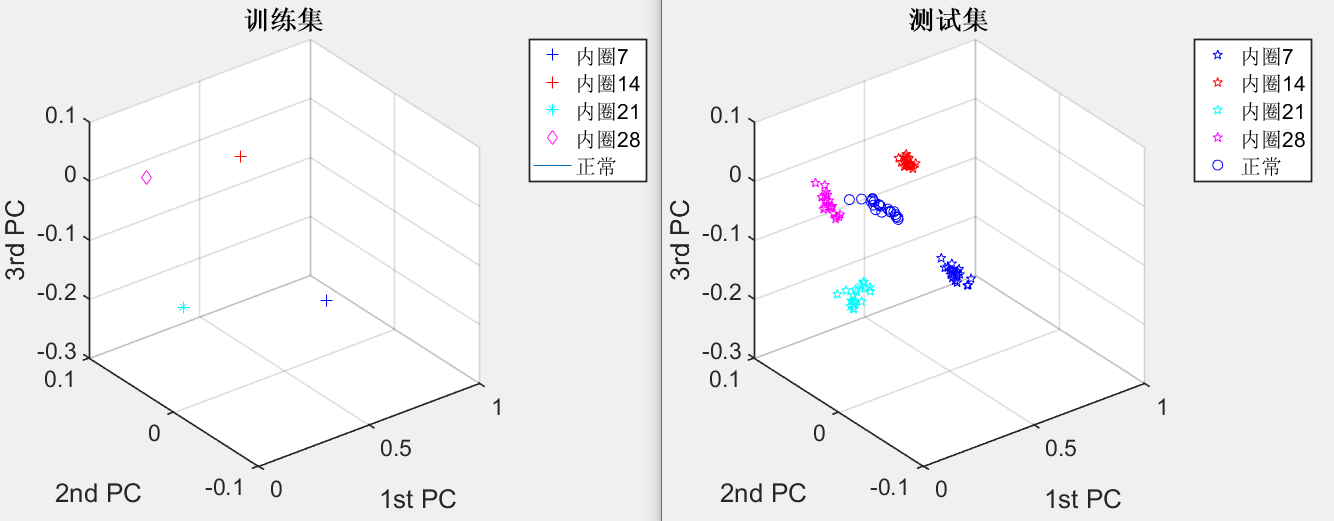
3.2.2 滚动轴承四种故障类型的识别 10

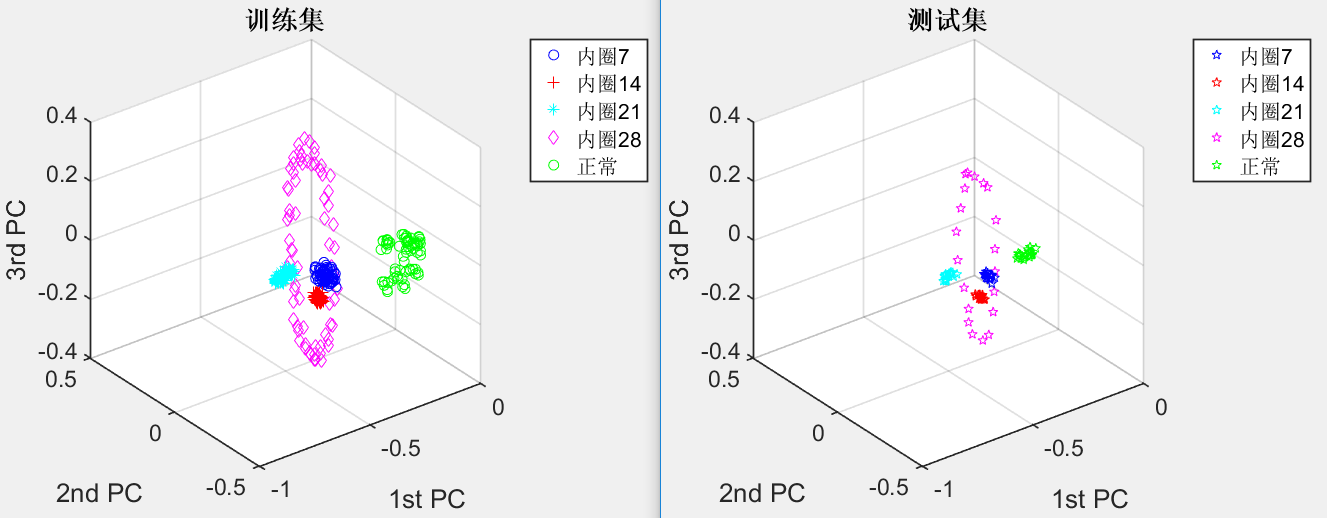
3.2.3滚动轴承五种损伤程度的识别 13

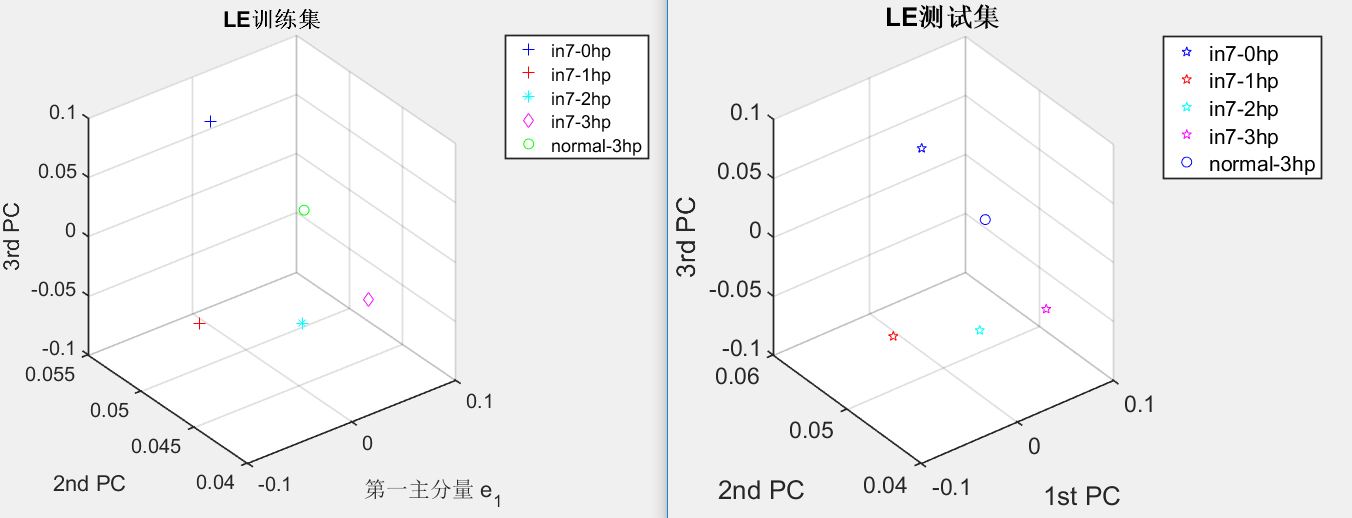
3.2.4滚动轴承在轻微故障程度下五种负载的故障识别 14

3.2.5 七种随机故障状态的识别 17

3.2.6不同样本下滚动轴承的故障识别精度 20

3.2.7三种算法在最高故障识别率时的参数设置 21

3.2.8特征维数d与近邻点个数K对识别精度的影响 22

第四章总结与展望 23

4.1总结 23

4.2展望 23

参考文献 24

致 谢 26

第1章 绪论

1.1 研究目的及意义

旋转机械在现代工业化的快速发展中具有重要作用，主要包括发电机，汽轮机，离心分离机等设备。与此同时，复杂的结构增加了制造成本，高速设备增加了动态负载，它加速了设备的损坏;随着集成度不断提高，功能更加多样化，旋转机械设备的结构和各部分的连接变得更加复杂，这也导致增大了事故发生率^[1]。如果旋转机械设备发生故障时，它不仅会影响产品正常生产的质量，也造成巨大的经济损失。更为严重的可能会造成人员伤亡以及环境的污染,同时也会对社会造成恶劣的影响^[2]。如最近的波音737max的印尼狮航和埃航事故,造成了较大的社会影响。因此，旋转机械故障诊断是现代机械工业的发展中越来越重要的组成部分。然而，由于生产设备的不断增加的复杂性和日益密切的内在关系，设备运行监测和故障诊断的难度越来越大。基于感觉器官，简单的仪器和工作人员的个人经验诊断已经不能满足现代机械设备故障诊断的要求^[2]。

滚动轴承是旋转机械中经常发生故障的部件,其运行状态直接关系到国民经济的快速发展和科技生产力的安全稳定运行^[4]，所以对其进行诊断就尤为重要。在对滚动轴承进行故障监测和诊断的时候，会产生大量的非线性高维数据。传统的故障诊断方法就越来越难以有效的诊断出正确的故障状态，从而可能会给企业造成巨大的损失。流形学习具有处理大量非线性高维数据的能力，倘若能将流形学习算法应用到轴承故障诊断中去，可能会有良好的效果，这也给故障诊断领域带来新的活力。

1.2滚动轴承故障诊断技术的研究现状状

机械设备故障诊断学是通过对振动信号进行特征提取和模式识别的方法来实现机械设备故障诊断的一门学科,综合了数学，力学，物理化学，电子学，计算机科学等众多学科^[5]。它采用先进的传感器和信号采集设备来监控机械设备，并使用相应的方法和技术手段来收集信号。提取或变换以获得各种功能的信息，选择被该装置的运行状态中最敏感的状态的特征量，结合设备和故障机制来判断和预测该装置的运行状态。机械设备故障诊断的实质是模式识别的过程，主要包括采集振动信号、特征提取、模式分类这三个步骤。

滚动轴承故障诊断在本质上是一个故障模式识别问题。在诊断过程中，信号监测装置会产生大量的特征参数，从故障特征集中提取出可以推断出运行状态的特征子集,这一工作就是特征提取。目前故障诊断中常用的较为传统的特征提取方法有时域分析、频域分析、时频域分析等。

时域分析法需要靠经验和大量的数据,依此进行判断,但由于存在噪声,因此会影响时域指标,从而降低故障判断的准确率^[6]。频域分析法的基本原理是把时间波形进行分解，将其分解为单一的谐波分量，从而更容易观测到检测信号的波形特征参数和特征结构^[7]。时间 - 频率分析方法是分布在时域和频域的信息的组合，它描述了信号频率之间与时间的关系。这种方法适用于非线性的频率分量。

在这几种方法的基础上，又发展出了经验模态分解(Empirical Mode Decomposition,EMD)^[8]、傅立叶变换(Fourier Transformation,FT)^[9]等处理非线性、非平稳故障特征的技术，解决了频域分析可用于处理平稳线性信号，但对于非线性、非平稳的故障信号却不能充分提取其代表性信息这一问题。

在对数据进行识别的模式上，可分为聚类算法与分类算法两种，目前使用的聚类算法是属于无监督的学习方法，不需要预先标定样品的类别，常用的包括K-均值(k-means)算法、DBSCAN(Density-Based Spatial Clustering of Applications With Noise)算法等；而分类算法属于监督学习，使用有标签的样本进行学习，常用的有人工神经网络(Artificial neural network，ANN)算法、支持向量机(Support Vector Machine，SVM)等^[10]。但是这些算法都有还没有解决的不足之处，K-均值算法容易受噪声的干扰，ANN则容易陷入局部最优解^[11]之中，从而不能够找到全局最优解。

以上这些方法是以前以及现今常用的故障诊断方法，但大都有其局限性及一些尚未解决的问题。特别是对于高维非线性数据，更是罕有成效，是故在此引入流形学习这一先进方法来对高维非线性数据进行降维。

1.3流形学习与拉普拉斯特征映射在机械故障诊断领域的研究现状

流形学习的概念首先出现在主曲线表面的研究和统计领域内。它一旦出现，就引起了人们的广泛关注，并引起了机器学习领域的研究热潮^[12-14]。其优异的非线性降维能力和出色的效果已经成为分类预处理和数据可视化的重要工具，已经被广泛应用到社会的很多领域，如数据挖掘，生物医药，信息检索，计算机视觉和模式识别领域等。作为一种新的数据分析工具,流形学习的本质在于数据的局部线性逼近,从而从高维数据空间之中探求内在规律及整体结构^[15]。

在流形学习中，较为典型的流形学习算法有拉普拉斯特征映射算法(LE)、局部切空间算法（Local Tangent Space Alignment,LTSA）、等距映射（Isometric feature mapping,ISMOP）等,以上述算法为基础,许多研究人员对流形理论的算法又进行了深入地研究和推广^[16]。

LE算法是一种经典的流形学习方法，其在维护流形的局部邻域信息方面有良好的效果，并能反映嵌入在低维流形中的数据集的固有的几何信息，以便于数据的聚类处理。该算法的具有良好的特点，可以将原问题转化为求解特征值问题，它不需要迭代算法，求解过程简单，运算速度快^[17]。它可以在减少故障数据维数方面发挥很好的作用。

目前,提出的各种旋转机械故障诊断方法较多。太原理工大学李月仙、黄宏臣等人提出一种基于拉普拉斯特征映射算法的旋转机械故障诊断方法,提取隐藏在高维特征空间中的故障本质和规律，具有良好的识别效果^[18];大连理工大学王雷等人针对旋转机械的故障特征提取,提出了一种基于张量流形学习的时频故障特征提取方法^[19];梁杰君,张颖等设计了一种改进的经验模态分解方法,小波变换-集成经验模态分解,并基于此提出了一种基于多段特征融合的旋转机械故障分类方法；江丽和郭顺生提出了修正的内核边缘分析(MKMFA)算法，使KMFA对特征提取和模式分类更加鲁棒，进一步提高其分类能力^[20]。

1.4研究的基本内容、目标、拟采用的技术方案及措施

流形学习方法在故障诊断领域内已得到了广泛地应用。它不仅可以被用作用于非平稳故障信号的有效噪声降低的方法，但还可以提取用于状态监测和趋势预测。在故障诊断领域流形学习方法的应用非常广泛，值得深入研究。本文以流形学习理论以及拉普拉斯特征映射为基础,针对旋转故障诊断中存在的问题进行研究。本文的内容安排如下:

第一章,介绍旋转轴承故障状态识别的研究背景及意义。本文讨论了滚动轴承诊断面临的问题以及传统故障诊断方法的不足。简要介绍了流形学习中的拉普拉斯特映射及其在故障状态识别中的应用前景。

第二章介绍了流形学习方法和拉普拉斯特征映射方法，并阐述了该算法的理论基础和用法。

第三章,基于拉普拉斯特征映射的诊断研究。使用流形学习中的拉普拉斯特征映射算法(LE)对滚动故障信号进行诊断,在故障信号中的高位数据信号中提取出具有代表性的低维流形特征。

第四章,旋转机械状态评估。对使用基于LE算法的故障诊断方法的结果与传统算法诊断进行对比分析,分析故障原因,诊断故障结果。

第五章总结了研究工作和全文的结果，并期待着在旋转机械故障诊断方法的进一步研究方向。

第2章 拉普拉斯特征映射算法及基于该算法

的智能诊断模型

2.1流形学习方法与分类介绍

流形学习算法是2000年来出现的一种非线性学习方法，它能将高维非线性数据降维，找出隐藏在高维空间数据中的低维结构，找出其内在的流形分布。所以它一经出现便受到了人们的认可与密切关注，它是一个分类预处理和数据可视化的重要工具，在计算机视觉、信息检索、生物医学等很多领域被人们广泛应用^[21]。

旋转机械设备的运行数据中蕴含着故障特征信息，可以使用降维算法来对高维数据进行降维，提取其中的低维流形结构，而后再使用其低维特征进行故障判别是一个可行的故障诊断方法，在本篇文章中使用的拉普拉斯特征映射算法有良好的降维效果。

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：