摘 要

径向基函数神经网络（Radial basis function neural network，RBFNN）由于其简单的结构及通用的非线性函数逼近能力，被广泛的应用于各种非线性系统当中。而对径向基函数神经网络结构影响较大的参数包括中心点的选取、输出权值的大小以及隐层神经元的个数等。因此本文先使用标准粒子群算法对径向基函数神经网络进行优化，通过使每个粒子对应一个RBFNN，不断对以上各项参数进行调整并计算神经网络的输出误差，最终得到较好的RBFNN。本文还在此基础上对标准粒子群算法进行一定的修改，使其能够具有更高的求解精度，更加适应径向基函数神经网络的训练过程。此外，本文中的神经网络训练方法可以对隐层神经元的个数及其他各项参数进行同时的调整。最后通过将优化前后的神经网络进行比较，来对算法的性能进行分析。

关键词：径向基函数；神经网络；粒子群算法；

Abstract

The Radial basis function neural network due to its simple structure and the general nonlinear function approximation ability, is widely used in various types of nonlinear systems. The parameters that have great influence on the structure of RBF neural network include the selection of center point, the size of output weight and the number of hidden layer neurons. Therefore, this paper first used the standard particle swarm optimization algorithm to optimize the radial basis function neural network. By making each particle correspond to an RBFNN, the above parameters were constantly adjusted and the output error of the neural network was calculated. Finally, a better RBFNN was obtained. On this basis, the standard particle swarm optimization algorithm is modified to a certain extent, so that it can have higher solution accuracy and more adapt to the training process of radial basis function neural network. In addition, the neural network training method in this paper can simultaneously adjust the number of hidden layer neurons and other parameters. Finally, the performance of the algorithm is analyzed by comparing the neural networks before and after optimization.

Key Words：Radial basis function; Neural network; Particle swarm optimization

目 录

第1章 绪论 1

1.1神经网络背景介绍 1

1.2粒子群算法背景介绍 2

第2章 径向基函数神经网络与粒子群算法基础 4

2.1 径向基函数神经网络 4

2.2 粒子群算法 5

第3章 自适应粒子群算法设计 8

3.1 自适应粒子群算法 8

第4章 粒子群算法优化径向基函数神经网络设计 10

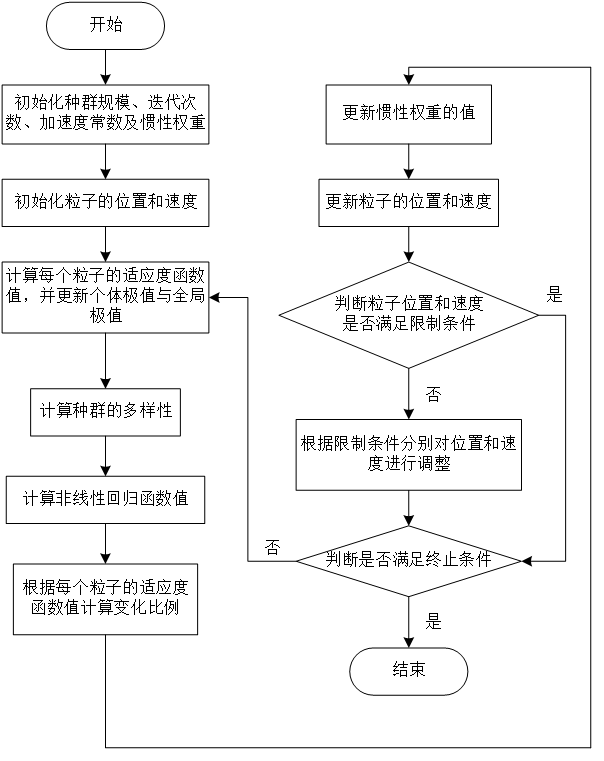
4.1 基于标准粒子群算法的神经网络优化 10

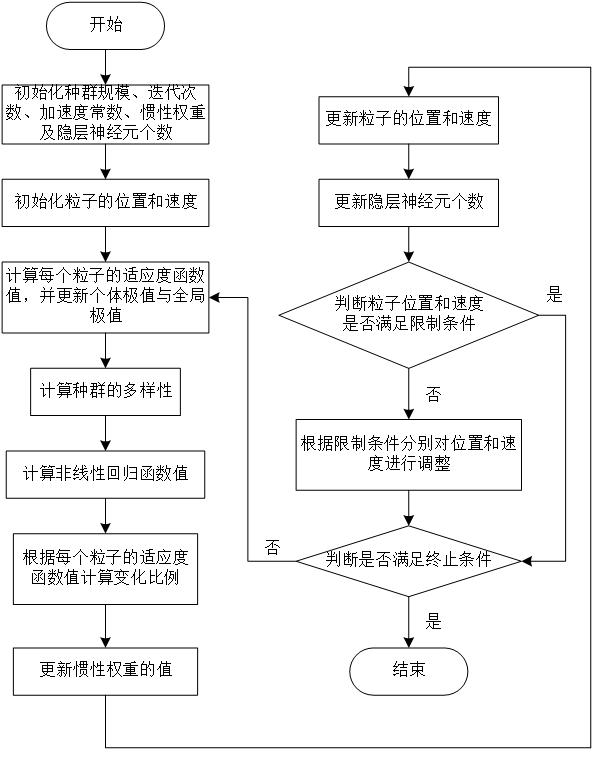
4.2 基于自适应粒子群算法的径向基函数神经网络优化 13

第5章 径向基函数神经网络测试 16

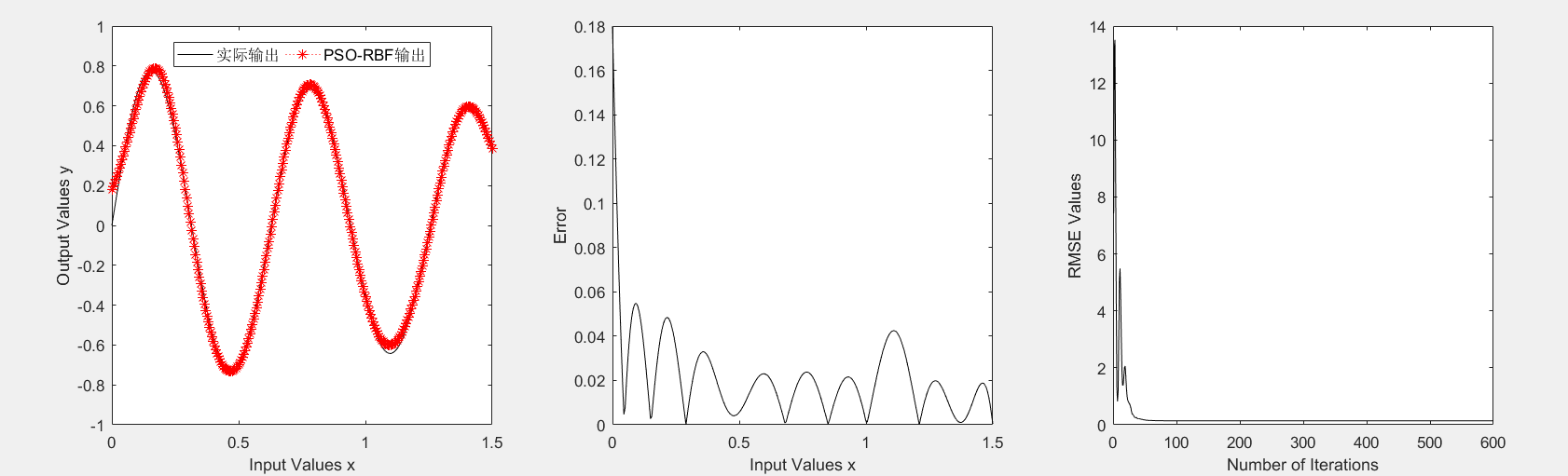
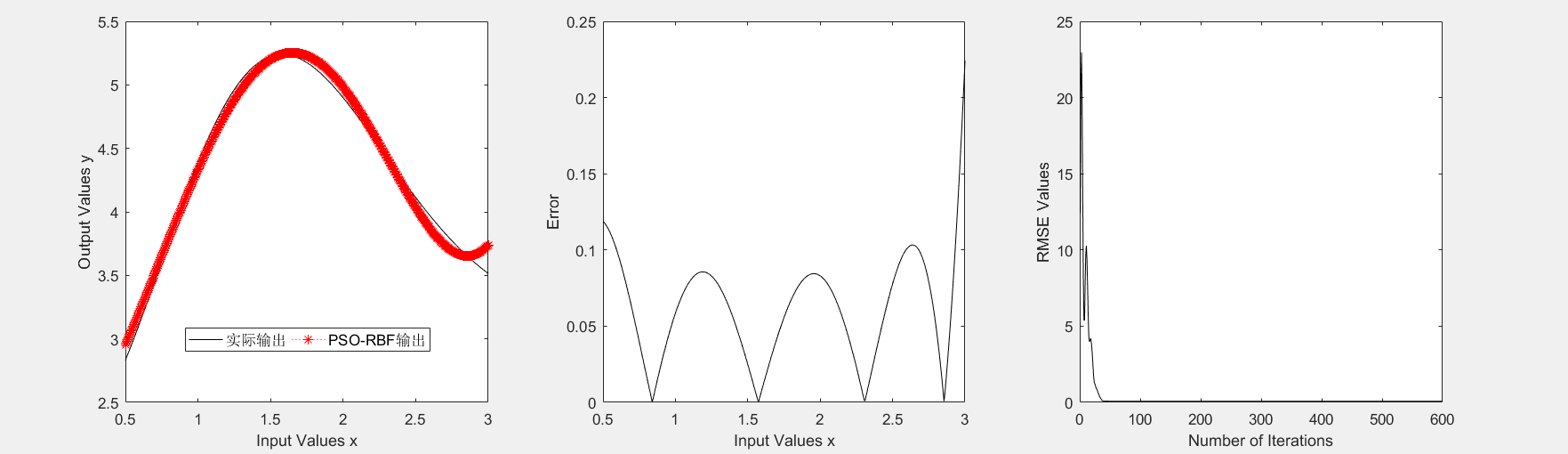
5.1 基于标准粒子群算法的径向基函数神经网络测试 16

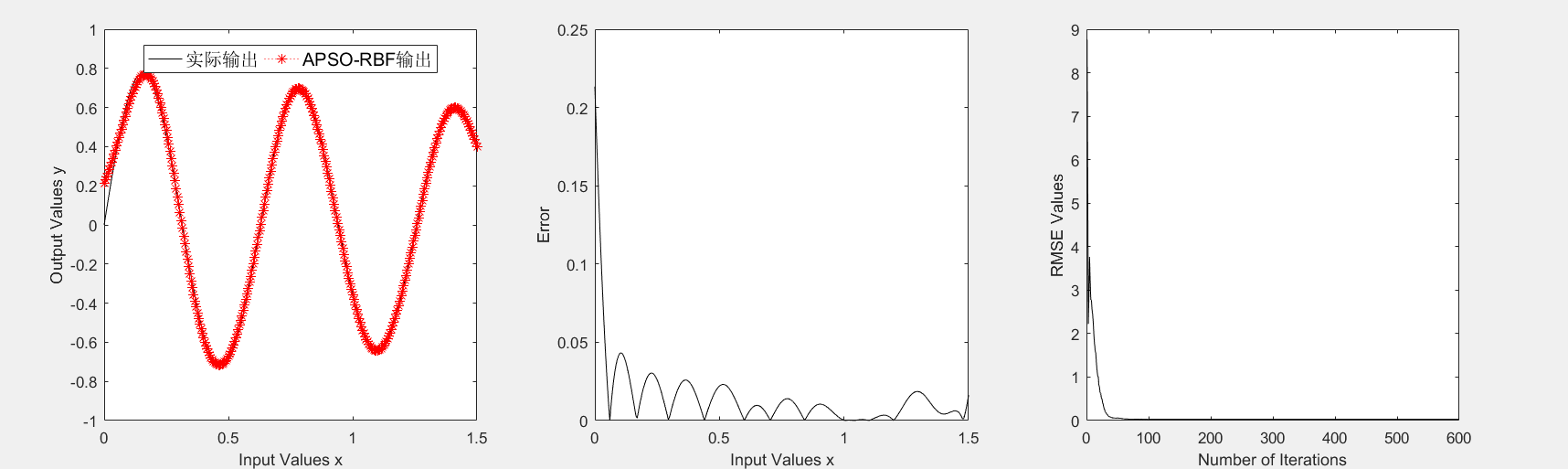
5.2 基于自适应粒子群算法的径向基函数神经网络测试 17

5.3 优化前径向基函数神经网络测试 18

5.4 结果分析 19

第6章 总结与展望 21

6.1 总结 21

6.2 展望 21

参考文献 22

致谢 24

第1章 绪论

本章将对神经网络及粒子群算法的国内外发展流程进行简要的介绍，并对其中具有代表性的研究进行详细介绍。

1.1神经网络背景介绍

神经网络是指由简单的处理单元所组成的大规模并行分布式处理器，它能够对大量的现有数据与知识进行存储，并且对其进行运用。神经网络的概念最早是由W.S.McCulloch和W.Pitts于1943年提出。而径向基函数神经网络（Radial basis function neural network，RBFNN）是由Broomhead和Lowe于1988年所提出的^[1], 并很快应用于监督学习的问题，如回归，分类和时间序列预测^[2]。由于RBF神经网络只有一个隐层，在对目标进行优化的时候，其收敛速度相对要快得多，此外，径向基函数神经网络通常被称为无模型估计器，因为它们可以用来近似所需的输出，而不需要数学描述输出在功能上如何依赖于输入。这使得径向基函数神经网络在函数逼近、预测、识别等方面得到了广泛的应用。实验证明，如果给定足够数量的RBF隐层神经元，径向基函数神经网络可以逼近任意连续函数。为了达到所需的近似精度，一些研究人员提出了多种RBF神经网络无监督学习或监督学习算法来调整模型参数(如：RBF中心坐标、RBF神经元宽度、输出权值)，确定网络大小(个数)^[3]。下面简要回顾一下有关RBF神经网络中参数调整及网络规模确定方面的文献。

C. Arteaga and I. Marrero提出了基于梯度和进化的方法对RBF神经网络的参数进行调整^[4]。在基于梯度的算法当中主要应用的是BP算法。然而，这种方法可能需要较长的时间来达到收敛，并且在寻找全局最优解的时候可能存在困难。之后又有人提出一种递归最小二乘法（RLS）与此相比，RLS算法则可以相较更快达到收敛^[5]。但是递归最小二乘法的数学运算更为复杂，同时需要的计算资源也就更多。为了解决上述问题，已经出现了一些更快和更先进的训练算法。J. Jiang 和 Y. M. Zhang提出了一种变长滑动窗口最小二乘(VLSWBLS)算法，以此来对递归最小二乘算法进行优化，并取得了较好的效果^[6]。Li，Peng和Irwin提出了一种快速递归算法（FRA），使用RBF神经网络模型进行非线性动态系统辨识^[7]。之后他们又提出了一种连续前向算法(CFA)来优化RBF神经网络的参数^[8]，这种方法有效的减少了内存的使用和计算复杂度，以此达到优化效果。Qiao和Han提出了一种只有前向计算(FOC)算法来调整参数，而不是采用传统的前向和后向计算^[9]。FOC算法使训练过程变得简单，降低了计算复杂度。虽然CFA算法、FOC算法和VLSWBLS算法的计算复杂度低于传统的优化技术，但它们都是更注重网络规模的选择而不是对参数的调整。近年来，一种改进的二阶(ISO)算法被提出用于在文章^[10]中训练径向基函数神经网络。该算法通过增加训练过程中变量的维数，可以获得较高的训练精度和较快的训练速度。而随着网络规模的增大，ISO算法的性能类似于Levenberg-Marquardt方法。与基于梯度的方法不同，进化算法在训练RBF神经网络方面时有更好的效果。进化算法的一个显著优势在于其全局优化能力。在^[11]中的结果表明，与现有的基于梯度的方法相比，进化算法可以摆脱局部极小值。但缺点是，这些方法可能会导致过拟合，计算复杂度较高，特别是搜索空间较大时。此外，对于算法的收敛性分析存在一定的挑战性，因此有时不能保证神经网络的收敛性。

径向基函数神经网络的构造，是一个需要对参数和网络规模同时进行确定的优化问题。径向基函数神经网络的结构对计算复杂度和通用性的影响是一个重要问题^[12]。因此，优化RBF网络的结构以提高性能至关重要。为此，人们设计了许多增长或减少隐层神经元的策略和算法。例如，Huang等人提出了一种顺序学习算法，称为增长和削减RBF (GAP-RBF)算法^[13]。通过对GAP-RBF的原始算法进行改进，提出了一个更高级的模型GGAP-RBF算法。GAP-RBF算法和GGAP-RBF算法都使用了一种同样的策略，该策略利用隐藏神经元的“重要性”，并将其与学习精度联系起来^[14]。这两种算法得到的RBF神经网络结构相对简单，计算时间也较少。但是，这两种算法都需要一套较为完整的训练样本^[15]。近年来，基于神经元活动和相互信息，Han等人研究设计了一种柔性结构的径向基函数神经网络 (FS-RBFNN)^[16]。实验结果表明，FS-RBFNN算法能够生成结构紧凑的径向基函数神经网络。Su,等人提出了一种新的径向基函数神经网络结构，利用区间竞争聚类算法成功地对符号区间值数据进行建模^[17]。在此基础上，提出了一种基于序列投影的元认知学习算法(PBL-McRBFN)^[18]。该PBL-McRBFN算法是受人类元认知学习策略和样本知识的启发而提出的。除了以上这些之外，还有许多的自组织RBF神经网络的算法和探究，需要注意的是，在这些算法中，大都不能对动态网络结构的参数进行调整。

为了能够同时对径向基函数神经网络的参数和网络大小进行优化，进化算法得到了一定的应用，从理论上讲，进化算法的最大优势在于它具有全局搜索的能力。其中粒子群算法(PSO)得到了更为广泛的应用，因为它比其他进化算法如遗传算法、差分进化等更快地找到最优解。为了解决训练时间的问题，Feng提出了一种基于粒子群优化(PSO)的自组织RBF神经网络^[19]。该方法构造了RBF神经网络的网络结构，加快了优化速度。Alexandridis等人提出了一种利用模糊和粒子群算法结合训练径向基函数神经网络的新算法^[20]。实验结果表明，所提出的自组织径向基函数神经网络能够达到很好的预测精度，并且实现较小的网络规模。此外，Lee等人提出了一种非线性时变进化粒子群算法(NTVE-PSO)来构造径向基函数神经网络^[21]，针对时间序列预测问题，采用NTVE-PSO算法同时确定径向基函数神经网络的最优参数和网络规模。在将粒子群算法应用于径向基函数神经网络模型优化时，现有的大部分工作都将评价准则从参数调整和网络规模确定的行为中分离出来。因此，如何建立一个统一的SORBF神经网络准则仍然是一个有待进一步研究的问题。除了这些与算法开发和实现相关的问题外，对算法收敛性的理论分析似乎相当具有挑战性。

1.2粒子群算法背景介绍

受神经科学，认知心理学，社会行为学和行为科学研究的启发，群体智能（SI）的概念，作为一种创新的集体和分布式智能模式，在1989年被引入计算和人工智能领域。其早期的应用主要是在没有集中控制或未提供全局模型的优化问题。这种算法的诞生是由于人们意识到，在当时现有的人工智能框架中观察到的许多局限性和缺点，都可能归结于这样一种假设，即智能是建立在个体的思想的基础上的，由此忽视了群体的基本贡献。因此，受到群居动物（如鸟类，鱼类，蚂蚁，蜜蜂和白蚁）的集体行为的启发而产生的群体的概念，被引入到研究多智能分布式系统中。群体是一群同类且简单的个体，它们每个个体都执行着相当基本的任务，并在它们自身和局部或全局的环境之间产生着相互影响，在这个模式当中并不存在一个中央控制。的确，尽管这些个体相对简单，并且自身能力有限，但它们通过信息共享的行为和交互模式，提供了实现解决问题的最终目标的能力。因此，这些算法作为受自然启发的、基于群体的算法而诞生了，这些算法能够为许多的复杂问题提供低耗、快速、强鲁棒性的解决方案。

粒子群优化算法最早是由Kennedy和Eberhart在1995年提出的。粒子群优化算法的灵感来源于在鸟群和鱼群中观察到的信息循环和群体行为。它是一种全局优化算法, 特别适合于求解在多维空间中某一点为最优解的问题。群体中的每个粒子不仅具有位置的属性，而且具有速度的属性，并且可以在搜索空间中移动。与其他群体算法不同的是,粒子群算法中的每个粒子的运动，不仅对其自己产生影响如：到目前为止自身所找到的最好的解,同时它也朝着由所有粒子发现的全局最好的位置移动，每个个体也是整个群体的子集。由此，粒子群优化算法可被应用于不规则的,含有噪声的的或随着时间动态改变的等多种问题的求解。

Clerc和Kennedy^[22]，Yasuda等人^[23]，Kadirkamanathan等人^[24]，以及van den Bergh和Engelbrecht^[25]对粒子群优化算法的收敛性和稳定性进行了分析研究。与此同时，关于参数设计、辅助操作、拓扑结构等的分析和研究也在进行着。

为了提高粒子群算法的加速收敛速度和避免局部最优。Ho提出了正交粒子群算法（OPSO）^[26]采用一种智能运动机制来调整粒子的速度。Gabriela Ciuprina等人提出了一种智能粒子群优化算法(IPSO) ^[27]，通过群体经验、禁忌避免、行为参数等对粒子群算法进行改进。Liang等人提出了一种综合学习粒子群优化器(CLPSO)^[28]，其利用所有其他粒子的历史最佳信息来更新粒子的速度。这种策略使群体的多样性得以保留，因此可以防止早熟收敛。在对粒子群算法进行改进的发展过程中，算法参数的控制和辅助搜索算子的组合已经成为三种最突出和最有前途的方法中的两种(另一种是改进拓扑结构)。

当然，除了参数控制和辅助搜素的研究，粒子群优化算法的拓扑结构也得到了广泛的研究。为了提高多峰值态问题的求解性能，Kennedy^[29]和Mendes^[30]分别提出了环形拓扑结构的LPSO和冯诺依曼拓扑结构PSO (VPSO)。此外，Hu和Eberhart^[31]以及Liang和Suganthan^[32]提出了动态变化的邻域结构，以避免固定邻域的不足。此外，在“完全知情粒子群”(full informed particle swarm, FIPS)算法中，使用整个邻域的信息来引导粒子的运动。之后提出的CLPSO允许粒子使用不同的局部最优解来更新其在不同维度上的飞行，进而在多峰值问题中提高求解性能。

第2章 径向基函数神经网络与粒子群算法基础

2.1 径向基函数神经网络

径向基函数神经网络是一种非常典型的三层神经网络，并且是一种前馈神经网络。例如图1所示，为多输入单输出的径向基函数神经网络，输入层由n个节点组成，隐含层由H个计算单元元组成，输出层由l个节点组成。在径向基函数神经网络中，采用径向基函数作为隐藏神经元。

径向基函数神经网络的第一层为输入层，由n个源节点组成，，其中n为输入向量x的维数。第二层为隐含层，亦称作隐藏层，由k个相同的计算单元组成，从数学上，每个单元都选择一个径向基函数作为激活函数。

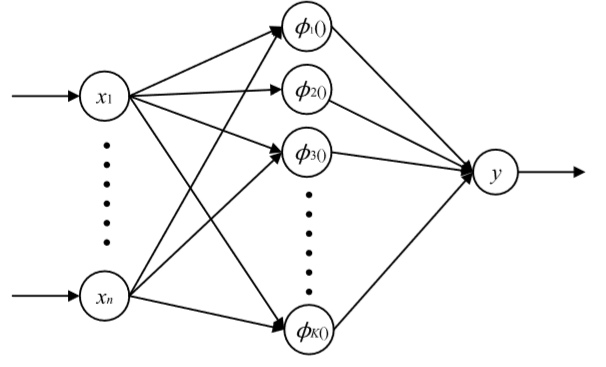
图2.1 径向基函数神经网络

第K个隐层神经元的输出表示为φ_k(t)，通常由归一化高斯函数定义：

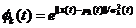（2.1）

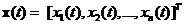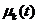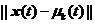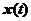其中是网络的输入，隐藏层的输入是标量权值和输入向量的线性组合，其中标量权值通常指定为单位值，即输入向量与隐含层神经元直接相连。表示第K个隐层神经元的中心，是和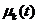之间的欧式距离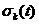，是第K个神经元的宽度。

第三层为输出层，输入向量由每个隐层神经元中的径向基函数映射。最终，在输出层通过隐层神经元的输出结果来进行线性组合，并产生最终的输出。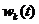为第K个隐层神经元到输出层之间的输出权值，最终的网络输出可由下式得出

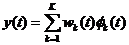（2.2）

在训练过程中，径向基神经网络的参数，即：隐藏神经元的中心和宽度以及输出权重，还有隐藏神经元的数量都将通过训练样本来进行调整。以上这些参数也是我们需要对径向基函数神经网络进行优化的部分。由于径向基函数神经网络的特性，只要拥有足够多的隐层神经元个数，径向基函数神经网络就能够逼近任何非线性函数。因此隐层神经元的个数对于径向基函数神经网络来说往往也是更为关键的因素，这也是我们需要进一步考虑该如何对其进行更合适的优化的根本原因。

2.2 粒子群算法

粒子群算法(Particle Swarm Optimization，PSO)是一种基于种群的优化技术，其中种群被称为群。对于最小化问题，一个群由许多粒子组成。每个粒子都通过一个矢量来表示的位置

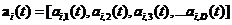（2.3）

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：