英语原文共 13 页，剩余内容已隐藏，支付完成后下载完整资料

铁路周边多层建筑车致振动的数值建模案例研究

摘要

近年来，随着振源附近建筑的日益增加以及人们对居住环境关注的提高，地面振动已经成为热门的研究话题。于是，建筑周边车致振动起到了重要作用。在车致振动预测中，已提出许多实际和理论方法，为研究Qaemshahr地区的铁路振动，采用一种2D有限元分析方法研究列车运动建模级振动对周边建筑的影响。数值模型的合理性已在高速列车的实际运行中被证实，结果表明：振动水平随轨道中心线距建筑地区距离的增加以及列车速度的减小而减小。入射波场振动频率最高达12HZ，频谱主频率在2.5到5.5HZ之间，在建筑基础区域车致振动引起的弯矩变化是可忽略的，轨道中心线距离建筑周边地区18M的地方被视为减小车致振动引起的干扰和环境影响的允许值。

关键词：车致振动；有限元方法；阻尼；振动水平

1、引言

过去几十年中，因高密度的城市化以及城区基础设施的快速发展，公路和铁路附近建筑数量大量增加，导致由于交通引起的地面振动对周边建筑物以及高科技基础设施的正常工作产生影响，使周边建筑产生了一些问题。它引起的振动包括在地表或地下的一系列将近2200HZ的地面振动。振动水平通常取决于汽车质量和速度，悬浮系统以及土壤性质。地下临近情况，地面和高架铁路系统引起的振动影响了建筑物安全性，人们的日常生活以及高科技设备的运行。因此，基于研究领域的重要性，振动效应研究很有必要。

近年来，许多分析和数值建模（Auersch,1994;Liao等,2005;Sheng等，1999；Metrikine和Vrouwenvelder,2000;Hall,2003;Forrest和Hunt,2006;Wanming等，2010）已用于研究车致振动，分析模型可以提供一系列持续的解决方案，而不是离散的价值，于是这最终提供了一系列取决于物理参数的长期作用。数值建模主要优势是考虑附近结构、土壤不连续性以及其他重要因素的影响。

Sheng等（1999）开发了一个模型，估计单谐波负载在铁路轨道运动时产生的地面振动。Yang等（2009）研究了列车以不同的速度移动时分层土的声波传播。Shen（2009）采用有限元的方法，研究了相邻卡车不规律的经过时建筑物的振动特性。Gao等（2012）基于不同距离下的列车特性提出多层土下振动的有限元方法。Triepaischaionsak和Tompson（2015）考虑列车-轨道相互作用，通过虚拟方法评价地面振动。

除了上述方法，许多实验室和研究已着手研究车致振动。Xia等（2009）通过原位试验研究列车振动对周围土地和建筑物的影响。周边地面和建筑物的速度水平，列车速度的影响，汽车荷载均被考虑在内。Zhang和Feng（2011）针对沪宁铁路，通过实验方法研究了高速列车引起的地面振动特性。

图1.地表车致振动传播过程

轴轮间距，质量和列车速度是行进中的列车带来的，影响轨道结构动力反应的重要因素。除此之外，还有许多由跟踪响应产生的振动来源。

铁路项目环境影响的评价系统中，振动假设是主要影响因素之一。在这之中，已发布像BS6470,DIN4150FTA这样的标准，应用于由地面产生的振动。尽管如此，直到现在，即使是通过数值分析，也依然有一些多层建筑车致振动的研究。周边土地由于铁路结构振动将被激励，并在入射波场中通过多层土把振动传播到建筑基础以及其他声波可及的其他结构，车致振动的传播过程由一些独特阶段组成，他们各自影响了振动特性并且在下一个阶段提供了一个不同的输入内容。多层土中振动传播过程如图1所示。

这项研究通过有限元方法，研究铁路车致振动在周边地面以及六层建筑上的影响。课题主要目的是研究车致振动中不同参数的影响，比如速度和加速度，轨道中心线至建筑边缘的距离，列车速度，汽车荷载等因素下，地面、建筑物的振动水平。这些重要参数正是本文的研究内容。

2、原理

动力荷载下体积的方程式为（Das,1993）。M是质量矩阵，X是位移矢量，C是阻尼矩阵，K是体积的刚度矩阵，P是动力荷载矢量。X是位移是速度是加速度，他们均随时间变化。方程式最后两个术语与静态变形有关。基于在此考虑的问题，M的组成部分（土，纯净水，以及其结构比如说铁轨，道渣，车辆等）被视为分块矩阵，土的阻尼和结构组成由矩阵C表示。事实上，材料阻尼是由摩擦和不可逆的变形（塑性和粘性）组成。随着塑性和粘性的增加，振动能量会逐渐减小。在矩阵C中，考虑弹性因素也是合理的。为确定阻尼矩阵，从实验中获得参数则更加困难。在动力分析中的Rayleigh阻尼法中，材料阻尼通常会考虑在内。Rayleigh矩阵在质量矩阵和刚度矩阵中建立了联系。(Zienkiewicz和Tayor,1991)，C为阻尼矩阵，M为质量矩阵，K是系统中不同组成的刚度矩阵，和为比例阻尼常数。矩阵K中，考虑了移动的体积刚度（不同列车元素），矩阵P为动力荷载（车致振动），对于质量比例阻尼（方程二中的第一个术语），低频振动被更多的抑制。对于刚度比例阻尼，高频振动被更多的抑制。这是因为在第一次的表述中，阻尼和频率成反比。在第二次的表述中，二者成正比。



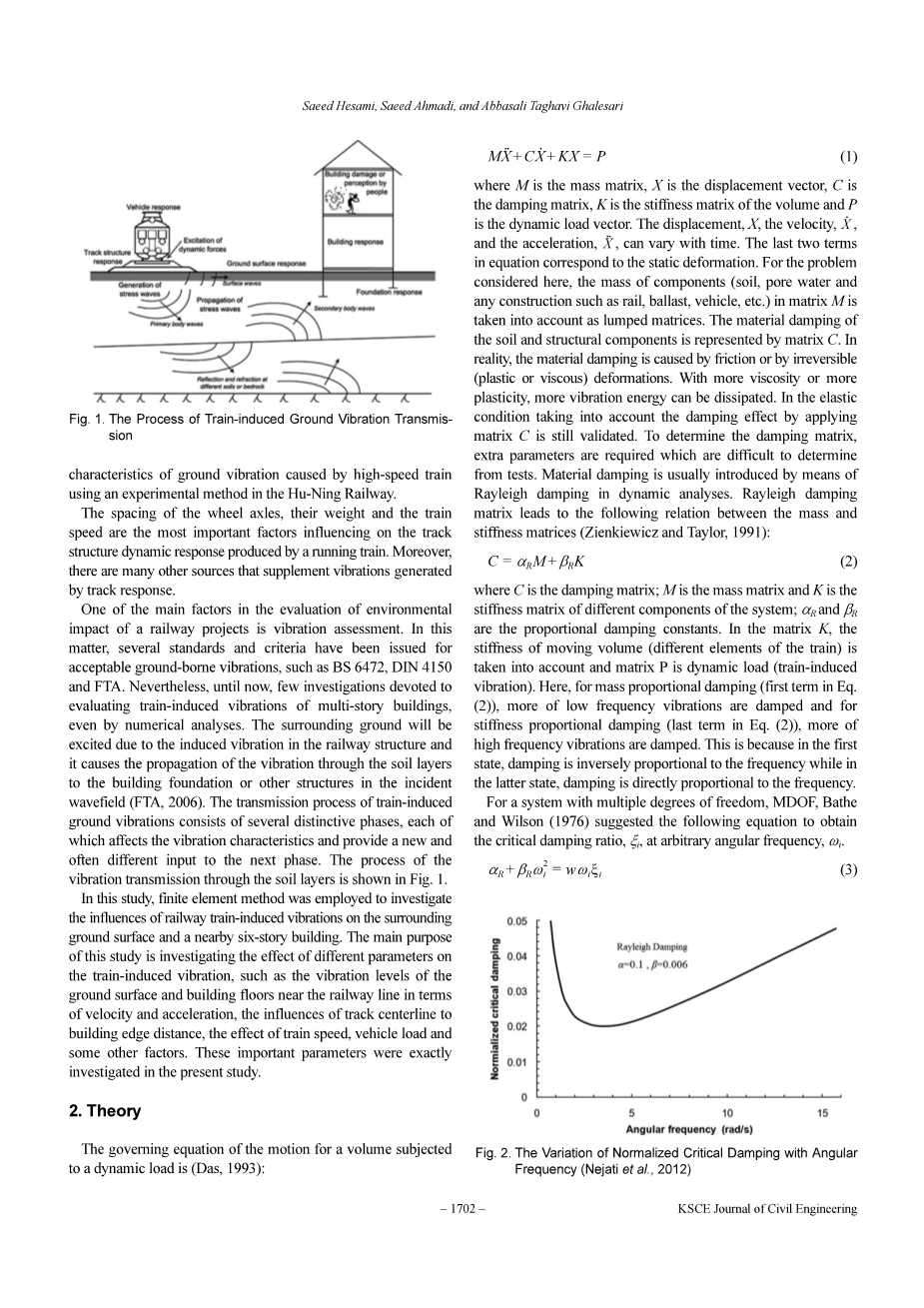
图2.标准临界阻尼随角频率变化情况（Nejati等，2012）

表1.不同土壤中与频率无关的衰减系数取值，（Yang,1995)

为解决系统自由度的复杂程度，MDOF,Bathe和Wilson(1976)提出下列方程来得出标准阻尼率和任意角频率，。当整个循环没有完成时，系统被称为临界阻尼，此时第一振幅的振动将会以指数方式消减至零。

在图二可出，Rayleigh阻尼可以通过计算出局部最小值，。Athanasopoulos（2000）提出估算阻尼率的经验公式：.是阻尼率，是Rayleigh波速，是Rayleigh的频率无关衰减系数。Yang（1995）在表1中提出了不同土壤中的取值。

3、土地性能和振动特性

3.1研究区域描述

Qaemshahr是Mazandaran的一个沿海城市，距离Caspian海27千米。这所城市中的地面振动评价十分重要。因为他是一个居住城市，居住在这的人们常受列车振动的影响，附近的一个六层建筑被视为研究对象（图3）他建于2005年，高18米，宽15米长36米，一层楼高3.8米，研究考虑列车不同速度经过时振动和户内户外不同水平的振动。

3.2土地研究



图3.铁路轨道和附近建筑物

为研究地基条件，钻孔取地下最大深度达四十米处的土，凿洞直径十厘米，锤击钻孔并用水冲洗。由结果可知，该地区主要是由黏性土组成，地下水位线位于地下三米处，层的渗透性估计为。

3.3铁路和列车配置

列车由七节车厢和二十八个轴线组成，由图4(a)可以看出，相邻轴线距离a=1.5m车厢长L=10m，每节车厢有两个转向架，每个转向架有两条轴线，每根轴线左右两侧各有一串轮子。传统有碴轨道用UIC60安装而成，并且每0.6m由单块混凝土软轨支撑。

表4（a)表示火车典型方案，火车动力方向，轴力情况。图4(b)表示车轮在样点上力的变化。

图4. (a)铁路车辆代表方案 （b）车轮轴向力变化情况

正如同图4(b)所展示的那样，第一个车厢的第一个轮子经过时产生了，之后消失，直至的到来。然后又是一个间隔。规范的轴力到了零，之后，第二个轮子又开始起作用产生了力。最终在间隔（,）中，规范的轴力取值为。从到后轴力再次消失。实际上，是一次循环结束的时间。因此，在零至中列车轴力大小可表示为。f(t)的功能上等同于的区间功能。如果f(t)是一个稳定的函数表达，那么他就可以延伸并在数值分析中体现出来。

3.4列车动力荷载

移动列车的动力模型在前面已经被立体的，全面的描述。尽管增加波传播时间和建模复杂程度，仍有可能把各种模型结合。为了减小分析时间，对火车模型进行简化（Garg和Dukkipati,1984)。然而，火车被视为纵向模型，火车法向力被视为点荷载。

表2.车致地面振动的重要影响因素（Hall,2003)

图5.列车动力荷载：（a)荷载类型a：车速80km/h，车身长度10m，车重100ton，（b)荷载类型b：车速80km/h，车身长度19.52m，车重50ton，（c)荷载类型c:车速160km/h，车身长度19.52m，车重100ton（Nejati等，2012）

表2表明车致振动的影响因素，其中有移动荷载来源。基于研究成果，对于移动荷载来源来说有两个独立的因素：准静态运动源(SMS)和动态运动源。目前，后者被视为在影响地面振动的重要因素。Sheng等（2004)结合了模型轨道的不规律性和车轮动态情况判断SMS。SMS激励符合列车轴线的静态荷载。

图5说明了在Neiati等（2012）得出的不同速度，长度，重量下的动力荷载，这正是表2中表明的影响车致振动的重要因素。

图6.选定地点布置方法

4、布置方法

火车轨道是由石灰岩底道渣层和斑岩的碎石层做成的，道砟层密度为2000kg/，泊松比为v=0.35杨氏模量为E=4000，布置方法在图6可以看出。A和B分别位于建筑边缘至轨道的最近和最远的距离，C表示土的自由场响应，D和E分别位于建筑的顶部和一层。

5、合理性

Hall(2003)通过现场测量证明了数值建模合理性，他在Ledsgaard演示了列车在142km/h下的车致地面振动。为决定土地刚度和材料阻尼，采用了跨孔法。同时使用静态和动态三轴试验，密度测定试验和动态弯曲元试验。基于不同土体研究，场地土特性如表3，布置方法如图7。场地土层的纵向断面和名称如图7，并根据图7布置方法进行建模和分析。除此之外，因列车信息不同，地面振动研究也采用不同的方法。质点位移由检波器信号表示，质点速度由伸长计信号表示。

路堤外由车致振动评估由垂直于加上正常荷载的轨道上的二维有限元所模拟的，土地模型由表3建模，铁轨基于Mindlin理论，由五节点梁单元，UIC60规则轨道建造，在0.001s内进行加载节点间距分析。假定列车荷载为图8的三角形脉冲，通过考虑铁轨上的观察点，可获得二维有限元模型的荷载情况。在观察点，荷载脉冲可在到的时间段内视为作用在铁轨上的点荷载。

表3.在Ledsgaard基于土壤研究的土壤特性总结

图7.在Ledsgaard基于土壤研究的土壤和铁路假定布置方法（Hall，2003）

图8.梁模拟轨道时有限元分析的外加荷载

图9.车速在142km/h下质点垂直速度时间历程的测量和二维有限元分析比对

图9表明距离列车不同距离下频域的测量数据，并与有限元分析结果进行了对比。两种分析方法的结果有惊人的一致，他们的不同可能是由土特性假定以及分析时忽视了横向尺寸造成。

6、数值建模

土中静态建模的本构模型是Mohr-Coulomb模型，而对动态分析则是线性弹性模型，使用线弹性模型是由于列车在土壤介质中动力波引起相关微小变形。土单元模型用十五节点的三角形单元建模。这些单元比数值建模中的结构单元更加有效。建筑楼板梁单元通过表4总结的特性建模，并将动荷载和静荷载加在单元上。铁轨（UIC60)和轨枕（混凝土轨枕）基于Mindlin理论由五个节点柱建模（Van Langen和Vermeer1991)，并将动荷载加在柱顶。

表4中土（软黏土），底渣和道渣的各项参数取自该领域的研究，文献和标准，底渣和道渣的材料特性和分类系统在ASTM C127 C131 C136等得以描述。同样，不同岩土工程顾问得出的材料试验参数决定表4中的模型参数。场地土特性（Qaemshahr,Iran)通过三个钻孔中的试验和现场测试决定。

表4根据弯曲和轴向刚度、泊松比（各自的EI和EA）表明建筑基础(混凝土楼板）和铁轨枕木的材料特性。通过混凝土杨氏模量（E=20GPa)，铁轨UIC60(E=206GPa)、枕木(E=9GPa)，以及他们的几何特性，可计算出弯曲度和轴向刚度。混凝土泊松比来自于标准实验结果，对于枕木而言，这个数值可通过考虑了相同杨氏模量的已知关系计算。

表4.应用于FE分析的材料特性

建模中考虑土-结构动力相互作用。结构和土之间的联系和铁轨和土的联系十分粗糙，以至于没有结构和土体有限元节点的相对运动可取代他们。接触面通过与土体材料相同材料特性的薄层界面单元建模。两个界面联系产生的剪切力和轴向力由修正后的Coulomb摩擦理论计算。尽管土体模型使用了相同的网格尺寸，但在土壤-结构，土地-铁轨和土-底碴表面中的网格细化中却很快解决。

为防止底部刚性层模型转变，模型底部受到约束，横向边界向下移动来模拟土壤沉降。吸收边界条件用于吸收动力荷载带来的压力增量，否则将会在土地介质内部响应。边界上用阻尼器而不是某一方向的固定物，在轴向剪切方向进行阻尼器和边界连接，边界情况基于Lysmer and Kuhlmeyer理论（1969）。比如，阻尼器X方向的轴向和剪切部分为，是材料密度，是各自的波速，和是提高吸收效能的松弛因子。这种方法被研究者（Nejati等，2012；Bathe,1995)频繁使用，在此次研究中也被使用。有限元单元孔和边界情况发的分布图在图十中可以看到。

图10.经典有限元网格和边界条件

为考虑材料阻尼，较早的使用了Rayleigh理论。这是一个与频率相关的Rayleigh阻尼独立于频率的频率范围。于是，主导频率必须在这个范围的。主要频率是模型的自然频率和荷载输入频率的结合。通过把重力荷载零阻尼的加到模型上，模型的自然频率可以通过在特定时间记录模

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[136906]，资料为PDF文档或Word文档，PDF文档可免费转换为Word