孔洞对纳米孪晶镁塑性变形机制的影响毕业论文
2020-02-18 10:05:22
摘 要
镁是最轻的金属结构材料之一,具有比强度、比刚度高和阻尼性好的特点,被广泛应于工业生产。由于镁中引起塑性变形的滑移系数量有限,孪生在镁中起到至关重要的作用。作为孪晶的重要组成部分,孪晶界对镁的微观变形的影响也值得关注。纳米孪晶金属的出现开辟了一个了令人兴奋的崭新的研究领域,近年来受到广泛的关注。纳米孪晶材料是一种在晶体中引入一些列相互平行的孪晶片层片结构的新型材料。基于此,本文首先利用分子动力学软件LAMMPS建立含孔洞的纳米孪晶镁模型,采用分子动力学方法模拟出含孔洞的纳米孪晶镁柱在拉伸荷载作用下的变形过程,并采用OVITO软件观察微观结构演化行为。最后综合多个加载数据的结果进行分析和汇总,最终得到纳米孪晶镁塑性变形行为。
研究结果表明:引入孪晶界会降低模型屈服强度,并在一定程度上阻碍孔洞的扩展及模型断裂,而孔径尺寸对加载应力峰值影响较小;孪晶界的阻碍作用从大到小依次是:加载方向与孪晶界相互平行、垂直、夹角为45°。
关键词:纳米孪晶镁;分子动力学;孔洞;加载方向;变形
Abstract
Magnesium is one of the lightest metal structural materials, which is widely used in industrial production.Twinning plays an important role in magnesium because of the limited number of slip systems that cause plastic deformation in magnesium.As an important part of twin, the effect of twin boundary on micro deformation of magnesium is also worth paying attention to.The emergence of nanocrystalline twins has opened up an exciting new field of research, which has attracted wide attention in recent years.Nanocrystalline twin is a new kind of material which introduces a series of parallel twin lamellar structures in crystal.Based on this, the molecular dynamics software LAMMPS is firstly used to establish a magnesium model of nano-twins containing holes, and molecular dynamics method is adopted to simulate the deformation process of nano-twin magnesium columns containing holes under the action of tensile load, and OVITO software is used to observe the microstructure evolution behavior.Finally, the plastic deformation behavior of nano twin magnesium is obtained by analyzing and summarizing the results of multiple loading data. The results show that the introduction of twin boundary can reduce the yield strength of the model, and hinder the expansion of the hole and the fracture of the model to some extent, but the size of the aperture has little effect on the peak of the loading stress.The obstructions at the twin boundary are as follows: the loading direction is parallel to and perpendicular to the twin boundary, and the included Angle is 45°.
Key words:Nano-twin magnesium; Molecular dynamics; The hole; Loading direction; Deformation
目录
摘要 I
Abstract II
第1章绪论 3
1.1 纳米孪晶金属 3
1.1.1 孪晶结构 3
1.1.2 纳米孪晶镁 4
1.2 研究内容 4
第2章分子动力学方法 5
2.1 分子动力学模拟基本理论 6
2.1.1 分子动力学模拟的发展 6
2.1.2 分子动力学模拟的基本原理 6
2.2 分子动力学模拟算法 7
2.2.1 分子动力学模拟算法的原子势函数 7
2.2.2 分子动力学模拟的积分算法 8
2.2.3 分子动力学模拟的边界条件 10
2.2.4 分子动力学模拟的系统 10
第3章含孔洞纳米孪晶镁变形行为研究 12
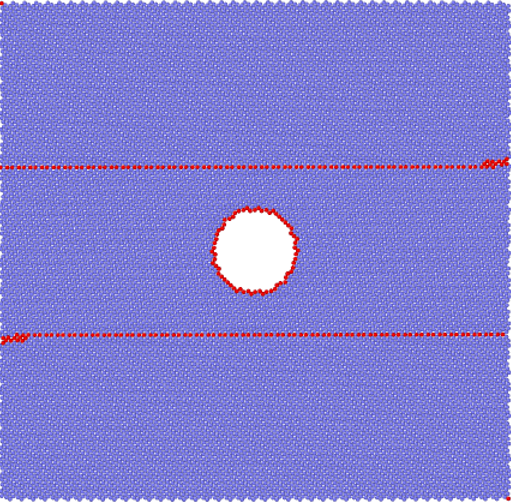
3.1 建模 12
3.2模拟方法 14
3.3孔洞对纳米孪晶镁变形行为的影响 15
3.3.1 含孔洞镁单晶变形行为 15
3.3.2 含孔洞纳米孪晶镁变形行为 16
3.3.3 孔洞对纳米孪晶镁变形影响的综合分析 19
3.4加载方向对纳米孪晶镁变形行为的结果讨论 21
3.4.1加载方向垂直于孪晶界 21
3.4.2加载方向与孪晶界夹角为45° 22
3.4.3加载方向与孪晶界平行 24
3.4.4加载方向对纳米孪晶镁变形影响的综合分析 26
3.5本章小结 27
第4章结论与展望 29
4.1 主要结论 29
4.2 工作展望 29
参考文献 30
致谢 32
第1章 绪论
1.1 纳米孪晶金属
1.1.1 孪晶结构
在晶体生长和制备过程中,孪晶的形成根据生成条件分为两种,一种是某一晶体的两侧原子在形成镜面对称时,在对称轴面处产生;另一种是两晶体的原子互相形成镜面对称时,该对称晶面即为孪晶面。孪晶界(Twin boundary,缩写TB)是一种比较特殊的晶面,当晶体在荷载作用下发生塑性变形时,基体与孪晶之间产生的晶面,而且该晶面两侧的晶体相互形成镜面对称。
孪晶界依据孪晶界两侧的原子排布规律可以分为共格孪晶界(Coherent twin boundary,缩写CTB)和非共格孪晶界(Incoherent twin boundary,缩写ITB)。
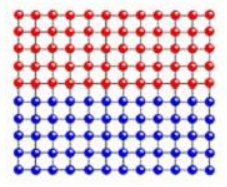
①共格孪晶界[1](CTB)是指晶体中孪晶界两侧的原子排布规律化,两侧原子在孪晶界处形成镜面对称,该孪晶界的能量相对比较低,该原子示意图如下图1-1所示:
|
图1-1 共格孪晶界示意图 |
②非共格孪晶界[2](ITB)是晶体中孪晶界两侧的原子与孪晶界不能形成镜面对称,孪晶界两侧的原子排布没有规律。该孪晶界的能量比起共格孪晶界会比较低,该原子示意图如下图1-2所示:
|
图1-2 非共格孪晶界示意图 通常情况下,材料的晶体结构与理想的晶体结构存在一定的差异,会存在许多的缺陷[3]。根据缺陷的类型不同,可以将这些缺陷分为点、线、面缺陷等。 |
1.1.2 纳米孪晶镁
镁(Mg)具有比强度、比刚度高、阻尼性好和易于回收等优点[4],因此主要用来制造轻质金属合金,也可以作为汽车、快艇、飞机等机械的合金材料。现阶段,镁及其合金产品大多采用铸造方式获得,深加工的镁金属比较少,在铸造过程中会形成一些孔洞、缩松、掺有杂质等缺陷,这些缺陷会对镁的应用造成各种限制[5-8]
随着时代的发展,人类对材料的性能要求逐渐提高,造成的结果导致金属以及普通的金属强化已经不能适应新的发展需求,故需要在原有的金属基础上,采取适当的强化措施。传统的金属强化模式通常分为四类:
其一是固溶强化,具体操作可以融入其他溶质元素;
其二是第二性强化,包括弥散强化和沉淀强化等;
其三是细晶强化,具体可以采取振动或者变质处理;
其四是加工硬化,具体方法可以采用冷拉,也可以称为冷作硬化;
但经过实验的分析,这些普通的金属强化途径虽然增强了金属的强度、硬度和抗畸变能力,但是都影响到了金属材料的其他力学性能,比如金属的塑性以及韧性的降低[9]。
由于传统的金属强化存在的一系列缺陷,科学家将目光转向了微结构层次的强化模式,其中比较突出的有纳米孪晶金属,它的出现为金属强化打开了新的领域,利用纳米尺度孪晶界面实现材料的强化可以避免上述的缺点,近年来一直受到广泛的关注[10-11]。纳米尺度共格孪晶界对金属的强化原理有两种:其一是它可以阻碍金属在荷载作用下位错的产生,与传统晶界的强化效果有异曲同工之处[12];其二是共格孪晶界附近可以提供丰富的位错储存空间,与传统的强化效果不同 [13],从而保证材料在铸造和加载时分别具有足够的加工硬化能力和稳定塑性变形能力[14-16]。除了优异的强塑性能力外,在单调加载或者循环加载过程中,纳米孪晶金属还可以表现出比较好的结构稳定性[17-19]、高疲劳寿命和高疲劳持久极限[20]以及低疲劳裂纹扩展速率。纳米孪晶金属因为其独特的塑性变形机制不断地表现出其综合力学性能。经过大量的研究发现,决定纳米孪晶金属宏观性能的关键是位错-孪晶界的交互作用。
1.2 研究内容
本文所研究的是孔洞以及加载方向对纳米孪晶镁的变形机制的影响作用,通过建立合适的纳米孪晶镁模型,进行合理意义的加载,充分认识孔洞以及加载方向对纳米孪晶镁变形的综合影响,分析其塑性变形机制。本文是利用LAMMPS(Large-scale Atomic Molecular Massively Parallel Simulator)[21]软件模拟孔洞以及加载方向对纳米孪晶镁变形机制的影响,主要研究内容如下:
(1)以镁单晶材料为研究对象,首先研究孔洞对纳米孪晶镁变形机制的影响,利用LAMMPS软件编写相关程序建立合适的纳米孪晶镁模型,其中包含:
(i)含孔洞镁单晶模型;
(ii)含孔洞纳米孪晶镁模型;
(2)紧接着研究纳米孪晶镁在加载过程中加载方向对其变形行为的影响,选择含孔洞纳米孪晶镁模型为该研究方向的基础模型。其中按照加载方向与孪晶界的夹角从大到小分为:
(i)加载方向与孪晶界相互垂直;
(ii)加载方向与孪晶界成45°夹角;
(iii)加载方向与孪晶界相互平行;
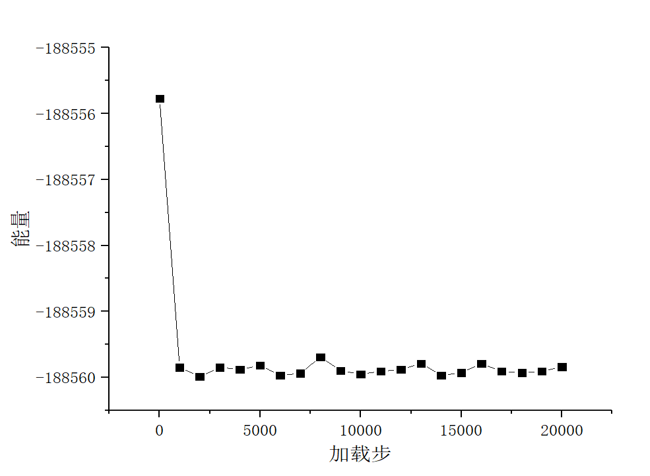
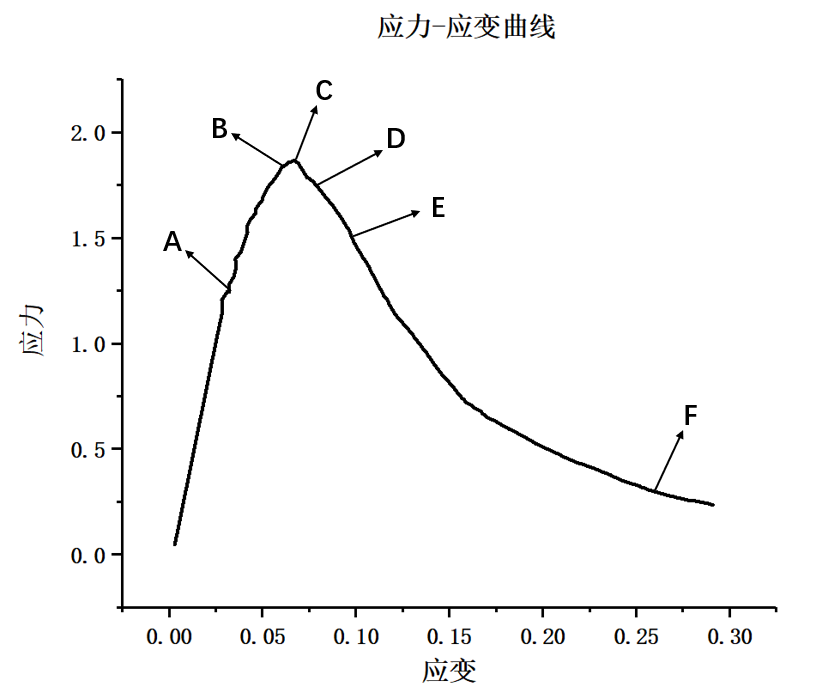
(3)然后利用LAMMPS软件设置合适的参数比如模型尺寸、晶格常数,温度等,并选择合理的镁金属势函数,再利用该软件编写相关加载程序对模型进行充分的加载,得到相关的数据文件;最后根据所做出的数据,利用OVITO和Origin分析纳米孪晶镁模型在加载过程中的微观结构变形行为以及应力-应变曲线。最后综合多个加载数据的结果进行分析和汇总,最终得到孔洞以及加载方向对纳米孪晶镁塑性变形行为的影响作用。
第2章 分子动力学方法
2.1 分子动力学模拟基本理论
2.1.1 分子动力学模拟的发展
分子动力学(Molecular Mynamics,简称:MD)是一门进行微观分析的综合技术,它的理论以物理,数学和化学的相关知识为基础不断发展进步。MD模拟方法正是基于牛顿经典运动学原理以及应用力场的变化进而发展起来的,可以描述微观粒子在不同温度下的运动变化,本文的研究采用的便是MD模拟。
MD模拟方法的发展历程要追溯到二十世纪中期,第一次采用MD模拟方法是在1953年,Metropolis[22]等人在国立实验室模拟处理统计力学相关物理问题。之后MD模拟方法开始出现在研究者的视线里,紧接着Alder[23]等人通过计算机进行构型积分,进一步计算体系宏观统计量,这是研究者首次借助该方法研究物质的宏观特性。随后Wainwright[24]等人利用MD模拟方法对硬球分子进行了模拟计算。在1960年,计算机模拟第一次在计算材料科学进行运用,Gibson[25]等人利用此方法研究得到晶体材料的辐射损伤原理。之后,在研究计算材料科学的诸多科研人员陆续加入到了利用MD模拟方法研究物质的性质这一行列中。
但是当时的计算机技术处于萌芽阶段,利用计算机模拟研究在时间和空间尺度上受到很大的限制。一直到二十世纪八十年代以后,随着愈加完善的势函数的提出以及计算机技术的蓬勃发展,MD模拟方法逐渐出现了新的生机。利用MD模拟方法研究的过程中,研究者一方面可以得到粒子在体系中的运动路径,另一方面可以在各个时间段对粒子进行观察。对粒子运动的研究,不仅可以了解到体系的微观变化,而且可以用来解释实验中大量的宏观现象。因此,MD模拟方法可以说是一个沟通微观世界和宏观世界的重要桥梁,应用于诸多科学领域。
2.1.2 分子动力学模拟的基本原理
MD方法的基本原理是把客观存在的宏观物质看做由很多个原子(分子)组成的的粒子系统,该系统中的粒子运动均遵守牛顿运动定律。在计算过程中我们首先要建立数学模型,把物质的微观结构、系统中粒子间的作用力和牛顿力结合在一起,然后在模拟得到其中任意一个粒子的运动信息后,就可以求得这个系统中其它粒子的位置、受力情况以及速度等信息,最后再利用分子统计物理学进行粒子系统的宏观动态模拟研究。其中牛顿运动学方程如下:
其中,i和j为系统中的任意两个粒子的序号,表示第i个和第j个粒子之间的距离,、、分别表示第i个粒子的质量、加速度、速度,表示体系中其他粒子对i粒子的作用力,除了质量其余的符号均为矢量。采用相关势函数对求导可以得到粒子i所受到的力,由公式表示:
其中,U是粒子系统所采用的势函数,在具有足够多粒子的系统中,每个粒子的受力与速度表达式如下:
MD模拟方法也也可以用统计力学的方法描述,即通过求解运动积分方程,进一步求得体系的空间分布,即系统。
2.2 分子动力学模拟算法
2.2.1 分子动力学模拟算法的原子势函数
在MD模拟中,势函数是主要用来描述粒子之间的相互作用,因此模拟结果的准确性取决于所选用的势函数对粒子之间相互作用描述的准确性。粒子之间的势函数精度和一般性很难得到普遍意义的满足,由于物质系统的复杂性和粒子之间的相互作用不同所导致,故一般采用理论推导计算或者通过实验所得的数据拟合求得。MD模拟方法的发展一定程度上取决于势函数的发展,势函数再发展过程中,先后出现了对势和多体势。对势与多体势的不同是在描述选定粒子间的作用力,对势认为粒子只与相近的粒子有作用力,与其它粒子间并没有作用力,这种势函数可以使用的范围很小,很明显在本研究中也并不适合;多体势认为粒子之间都是存在一定的作用力的。因此,采用多体势进行模拟,能得到更加精确的模拟结果,本文的研究所采用的便是多体势。
(1)对势
对势通常是用来描述一般的无机化合物原子之间的相互作用。现在广泛应用的对势有Morse势、Lennard-Jones势、Jones势和Born-Mayer势。
以L-J势函数为例,其势函数具体形式如下:
其中,表示第i个和第j个粒子的距离;是粒子之间相互作用的强度,即势阱的深度;是长度标度,表示的是粒子间相互作用势为零时所对应的距离。由于其计算简单和效率高的优点,经常被广泛使用于描述气体的性质。
(2)多体势
多体势通常是用来描述金属原子之间的相互作用。如今广泛采用的多体势有Finnis-Sinclair势(F-S势)、Embedded Atom Method势(EAM势)、MEAM势和Tersoff势。在多体势中, EAM势函数大多数情况下都被用来模拟金属原子之间的相互作用,能够很好地描述金属体系的结构、力学以及热力学的性质,并且计算效率高。在本研究中,我们研究的是纳米孪晶镁,故采用的是EAM势函数。
其中EAM势函数为例,其具体表达形式如下:
其中,表示镶嵌函数,表示所有原子的所有电子除了第i个原子之外在第i个原子处产生的电子云密度之和。f(r)表示原子的电子密度,表示原子的硬化参数,表示原子的拟合参数。
2.2.2 分子动力学模拟的积分算法
在数值模拟的计算过程中,我们经常会采用一些积分算法来求解粒子的微观信息,由于体系的运动方程不能直接通过理论求解,需要数值离散求解。不同的积分算法,适用范围及优、缺点不同,因此选用合适的积分算法在分子动力学模拟中显得至关重要。
在分子动力学模拟中经常采用的积分算法有:Verlet算法和Gear predictor-corrector算法。在一般情况下,当Verlet算法是被用来做较大积分步长的计算的时候,计算误差较小,而当Gear predictor-corrector算法是被用来选用较长积分步长的情况的时候,计算误差比较大。而速度Verlet(Velocity Verlet)算法是Verlet算法的改进,这种算法在实际模拟中经常采用,被如今流行的很多分子动力学模拟软件所认可。
以Verlet积分算法和Velocity Verlet积分算法为例,简单介绍算法的原理。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: