英语原文共 10 页，剩余内容已隐藏，支付完成后下载完整资料

锥形山顶撞击对远射雷电磁场的影响

侯文豪，张其林，王磊，张金波

摘要 本文利用二维有限值，在距闪电通道0.3至50km的距离范围内，探测锥形山顶，计算出地面雷电垂直电场和方位磁场。圆柱坐标系中的差分时域方法。研究发现，对于近距离和远距离观测，山峰高度和倾角对雷电辐射电磁场有显著影响。对于雷电辐射的垂直电场，超过几公里的远场（主要是辐射场分量）的增强是由于山地地形和平地之间的过渡中的反射过程，但是近场的近场减少。山地地形（主要是准静电场成分）是由于阴影效应，而不是由于这种反射。对于闪电辐射的方位磁场，不同山地地形的场值，包括山峰高度和倾角，都会增加近距离和远距离观测距离。

索引术语 雷电流，雷电电磁，山高，山倾角，传播路径。

1.引言

广泛使用的闪电定位系统提供从远程测量的电场或磁场估计的发光返回行程峰值电流。对于理论估计表达式，通常假设返回行程通道基本电流和辐射场彼此成比例，并且比例系数被确定为以完美的电导率击打平坦的地面[1]—[3]。但是，由于雷击的复杂性，闪电辐射电磁场沿着有限导电地球的过程和传播效应，使用场对电流转换因子（FCCFs）对雷击平坦地面似乎不适合闪电击中高大物体，特别是对于导电率较低的传播路径。例如，Azadifar等。 [4]利用在SantisTower（位于瑞士东北部）获得的当前数据，提出了欧洲雷电探测合作（EUCLID）网络的性能分析，发现EUCLID网络提供的峰值电流估算值比直接测量的高约1.8倍。此外，李等人[5]提出了一个理论分析，支持同时记录在Sntis塔测量的发光电流和在距离塔约15公里处测量的电场。他们的结果表明，Santis塔周围存在山地地形，导致辐射电场增强，这与EUCLID网络的过高估计是一致的。

到目前为止，已有大量关于撞击高大物体或山顶的闪电放电特性的研究。对于闪电击中高大物体的情况[6]—[17]，由于物体中的瞬态过程，电流波形在沿物体的不同高度处可能显着不同，并且可能表现出多于一个峰值（通常次级峰值大于初始峰值）。在远距离处，用于撞击物体的闪电辐射的电磁场可以变得大于撞击平坦地面的电磁场。然而，在物体高度或更低的非常近的距离处，发现撞击物体的电场相对于平坦的地面减小（例如，[8]，[14]）；Mosaddeghi等人也报道了这种阴影效应的实验证实。[15]

为了击打山顶（例如[5]，[18]—[21]），雷电辐射的电磁场与平坦的地面有明显的区别，这将对FCCFs产生显着的影响。雷电流峰值的估计。索托等人[18]，[19]提出了闪电辐射的电磁场，用于打击不平坦有损地面的不同配置，并发现了一个增强的垂直和水平电场分量，用于照射锥形山顶。距离非常近1公里。Khosravi等人^[21]进一步分析了闪电辐射的电磁场撞击位于平坦地面上的高塔和闪电辐射的电磁场撞击位于锥形山上的高塔之间的差异，并且发现与塔架在平坦地面上的情况相比，用于撞击锥形地面上的塔架的电磁场具有增强性。此外，山锥角和高度以及塔高对沿塔，闪电通道及其相应电磁场的电流分布有影响。

然而，Soto等[18]和Khosravi等的模拟结果[21]都在距雷击点（山顶）1公里的水平距离内，这对于估计雷电感应电压非常重要。实际上，为了分析雷暴过程或发光损伤事故期间的闪电时空演变特征，我们通常必须根据观测到的地面远场峰值来估计雷电流峰值。因此，研究雷电辐射电磁场对山地地形的传播效应，有助于提高雷电峰值估计的准确性（如闪电定位系统）。因此，在本文中，通过在圆柱坐标系中使用有限差分时域（FDTD）方法，我们将在观察距离处计算地面上的雷电辐射垂直电场和方位角磁场。在0.3至50公里范围内，以不同的高度和倾斜角度撞击锥形山地地形，并进一步详细分析不同山地地形对雷电辐射电磁场的影响，主要是由于反射过程中的影响。山地地形与平地之间的过渡。

2.方法

A.用于计算雷击辐射电磁场撞击山地地形的二维FDTD（2-D FDTD）模型

为了模拟非平坦地形对雷电辐射电磁场的影响，在圆柱坐标系中使用二维FDTD方法求解麦克斯韦方程[22]，[23]。本研究采用锥形山，如图1所示，其中h，w和theta;分别是山的高度，宽度和倾角，d是从闪电通道到观察点的水平距离。模拟尺寸为52kmtimes;3.5km，上边界和右边界由对称完美匹配的层吸收边界包围[24]。空间步长为Delta;r=Delta;z=5m，时间步长为8.3ns。闪电通道由垂直阵列的电流源模拟[25]，回程速度设置为v = 150m/mu;s。因为我们只是在传播到观测点后的最初6-7mu;s内对场进行分析，所以FDTD模型中的通道长度设置为1.5km，这足以计算分析窗口内的电磁场[21]。为了模拟FDTD方法中的非平坦地，采用共形FDTD方法[26]，[27]和电磁参数，如渗透率（mu;），电导率（sigma;）和介电常数（ε）在山与空气之间的边界单元中，考虑到单元边缘上两个中位数的比例来计算。图1还展示出了本文中使用的电磁场分量矢量的正方向。

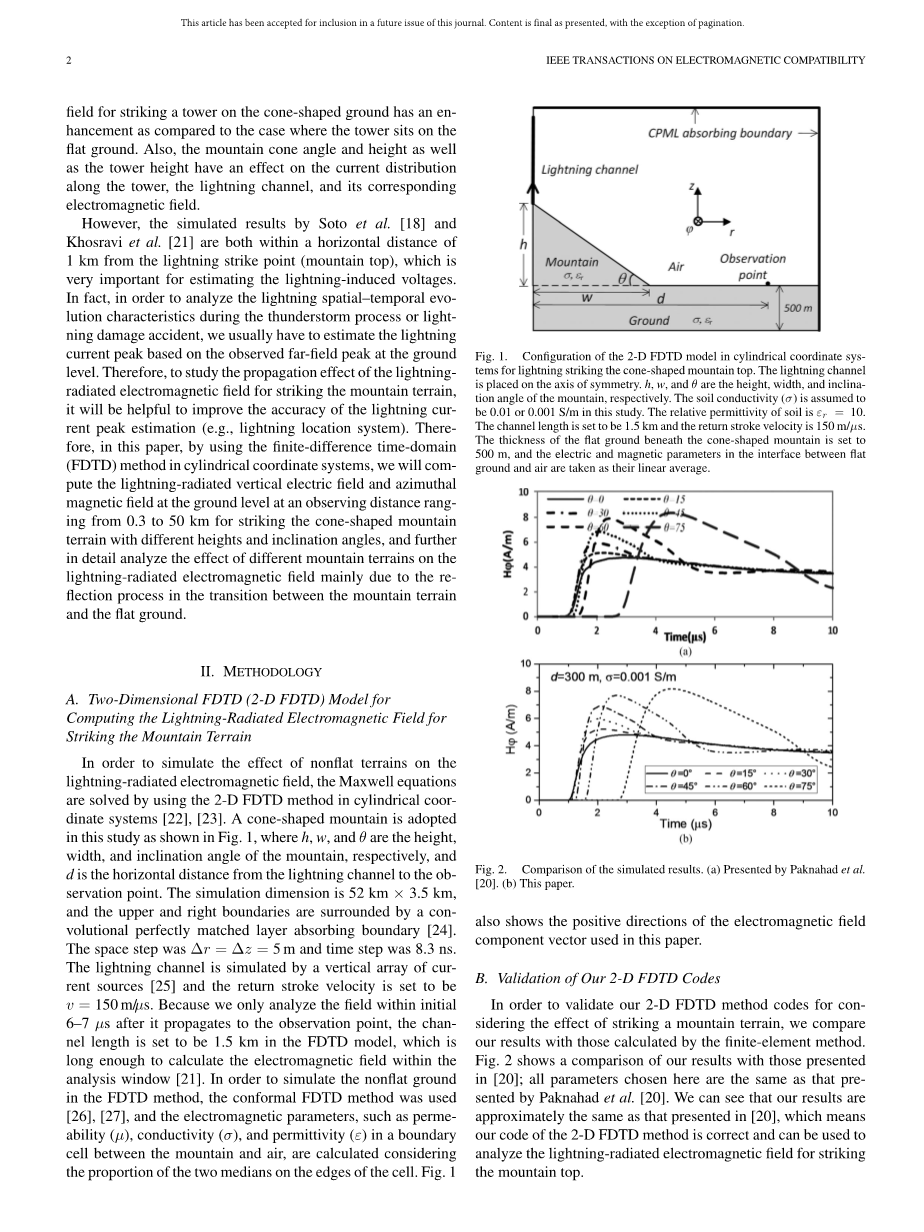
图1 圆柱坐标系中二维FDTD模型的配置，用于闪电击中锥形山顶。闪电通道位于对称轴上。h，w和theta;分别是山的高度，宽度和倾角。在该研究中，土壤电导率（sigma;）假定为0.01或0.001S/m。土壤的相对介电常数ε_r= 10。通道长度设定为1.5km，返回行程速度为150m/mu;s。锥形山下方平坦地面的厚度设定为500米，平地与空气界面的电磁参数作为线性平均值。

图2 模拟结果的比较。（a）由Paknahad等人[20]提出。（b）本文。

B.验证我们的二维FDTD代码

为了验证我们的二维FDTD方法代码以考虑撞击山地的影响，我们将结果与有限元法计算的结果进行比较。图2显示了我们的结果与[20]中的结果的比较；此处选择的所有参数与Paknahad等人提供的参数相同[20]。我们可以看到我们的结果与[20]中的结果大致相同，这意味着我们的二维FDTD方法的代码是正确的，可用于分析闪电辐射的电磁场以击打山顶。

图3 山脉对雷电辐射垂直电场的影响，范围从d=300m的近距离到d=50km的长距离。假设倾角为45°，地球的电导率范围为0.01至0.001S/m。

3.计算结果与分析

在本文中，我们选择了典型的后续返回行程通道基电流，峰值为12kA，最大陡度为40kA/mu;s，由以下Heidler[28]参数表示：I₀₁=10.7kA，tau;₁₁=0.25mu;s，tau;₁₂=2.5mu;s，I₀₂ = 6.5kA，tau;21=2.1mu;s，tau;22=230mu;s，n=2。改进的传输线模型采用指数衰减模型（MTLE）[29]，[30]假设 采用电流衰减常数lambda;=2km来表示沿通道的返回行程电流。

A.击中锥形山对雷电辐射垂直电场范围的影响从d=300m到50km。

图4 撞击山顶的垂直电场峰值与撞击平地的垂直电场峰值的比值

图3显示了在d=300m至5km范围内观察距离时撞击山顶对垂直电场的影响，假设倾角为45°，地球电导率范围为0.01至0.001S/m。假设闪电击中高度为300和1500米的山顶，从图3（a）和（b）可以看出，在山的底部，与水平地面相比电场明显减少。然而，随着观测距离的增加，撞击山顶的电场明显大于撞击平地的电场。撞击水平距离为3至50km的山峰的场峰明显较大，大约是撞击平地的1.75-2.60倍（见图4），这意味着我们应该更加注意利用观测到的远场，山地地形对雷电流峰值估计的影响。当然，有限导电地球的影响也非常明显，特别是在远距离（例如，d=50km）。

图5 不同（a）和（b）山峰高度以及（c）和（d）倾斜角对地面远闪电辐射垂直电场的影响

图6 闪电击中锥形山顶的垂直电场增强比，具有不同的（a）高度和（b）倾斜角

图5显示了不同山峰高度（见图5（a）和（b））和倾斜角（见图5（c）和（d））对远闪电辐射垂直电场的详细影响地面水平，图6进一步显示了撞击不同山地地形的场增强比。结果表明，较高且较尖锐的山峰导致较高的场峰值，并且随着山峰高度的增加，场地增强非常平缓或大致保持不变。例如，对于倾角为60°的山峰，当山峰高度超过500米时，比率保持在2.7左右（见图6（a））。然而，随着倾斜角的增加，增强比不断增加（见图6（b））。

图7 三种不同路径对远闪电辐射垂直电场的影响

图7进一步说明了三种不同波传播路径对雷电辐射垂直电场的影响。三条不同的路径具有相同的山峰高度，路径1具有45°的倾斜角度，路径2具有凹形路径，路径3具有60°的倾斜角度。发现倾角越大，场值越大。凹路2具有与倾斜角度为60°的情况类似的场值；因此，对于相同的山地地形，还应考虑不同倾角角度路径对雷电场的影响。

图8 闪电击中平地（左）和山顶（右）的垂直电场的时空演变特征。要点（f）中所示的A和B具有与山顶上的雷击点相同的直线距离（2km）。A点位于地面和B点在空中。（f）和（h）中的红色和黑色虚线分别代表反射波和入射波的波前。

图9 （a）静电场分量和（b）雷电通道及其图像产生的辐射场分量的极性。 在区域1中，雷电通道中的电荷产生的垂直静电场分量的方向与其图像电荷相反，但该区域接近正电荷，因此垂直静电场分量仍为正。 对于辐射场分量，雷电流及其图像电流都是向上的，垂直辐射场分量都是负的。

为了进一步了解在不同的观测距离上撞击山顶顶部对雷电辐射垂直电场的影响，图8显示了雷击平地的垂直电场的时空演化特性和山顶。我们可以看到有两个场区域，一个是正场值，另一个是负值，在本文中，向上电场被认为是正的。根据Biot-Savart定律，几乎在雷电电荷通道上方的磁场近似为零，远辐射垂直电场分量是放电正上方最弱的[31]，[32]。然而，区域1中的计算的场值主要是静电场分量，这是由于在非常近的距离处贡献的电荷再分布。从静电场点看，负雷击回程过程相当于正电荷的增加或负电荷的减少；因此，区域1中的静电场值是正的，如图9所示。然而根据TEM波，在区域2中，山地附近的静电场分量是负的，并且感应和辐射场分量也是负的。

此外，在雷击山地地形顶部后，可以看到当雷电场波到达锥形山与平面之间的过渡时，发生反射波（例如，参见图8（d））因此远场辐射场峰值变大。远辐射场分量是来自山顶（雷击点）的入射波和过渡时的反射波的叠加；图8（f）和（h）中的红色和黑色虚线分别代表反射波和入射波的波前。值得注意的是，山地附近的电场减少是由于山地地形引起的静电屏蔽效应，而不是由于过渡中的反射波。对于更高，更清晰的山地，基于物理中的图像电荷方法，我们很容易知道静电屏蔽效应会更多。

图10 地面和空中场场波形的比较

为了进一步分析波叠加特性，我们选择了两个与山顶雷击点相同的直线距离（2km）的点，一个位于地面上，名为A，另一个是空气中的B点，如图8（f）所示。从图8（f）中，我们可以发现入射波和反射波同时到达地平面上的观测点A。然而，对于空中观测点B，入射波首先到达然后到达反射波。因此，从波形特征来看，如图10所示，A点的场波有一个峰值点，而B点的场波有两个峰值点，这将导致确定时域中的雷击回击场波到达时间的一些困难。

此外，我们可以看到波浪沿着地球表面传播，对于地面上的观测点，通过比较图8（a）和（c）与图8（b）和（d），可以看到由山地地形引起的时间延迟。这意味着在使用到达时间方法时，我们应该更加注意山地地带引起的闪电位置误差，特别是当观测点靠近山地地带时。

B.撞击锥形山对闪电辐射方位角磁场测距的影响从d=300m到50km

图11 在d=300 m至50km的观测距离内撞击山顶对闪电辐射方位磁场的影响，假设倾角为45°，而地球的电导率范围为0.01至0.001S/m。

图11显示了在d=300 m到50km范围内的观测距离上撞击山顶对闪电辐射方位角磁场的影响，假设倾角为45°和地球的电导率范围从0.01到0.001S/m。结果发现，对于任何目标距离，磁场强度明显大于撞击平坦地面的磁场强度，这与垂直电场不相似，因为磁性元件由感应和辐射组件组成，锥山与平地之间的过渡反射会增加磁场强度，当锥山越来越尖锐时，反射越大，相应的磁场值越大。

图12 闪电辐射的方位磁场的时空演变特征，用于撞击平坦的地面（左）和山顶（右）

图12进一步显示了闪电辐射的方位磁场对于平坦地面和山顶的时空演化特征。可以看出，几乎直接位于雷电荷通道上方的磁场近似为零，并且场波在锥形山地地形和平坦地面的过渡中具有明显的反射过程，并且磁场值较大时山的高度和倾角更大。

C.击中被山脉环绕的锥形山对雷电辐射电磁场的影响

图13 （a）二维FDTD模型配置的横截面视图，用于闪电击中由一连串山丘环绕的锥形山峰，（b）相应的三维视图。h₂和theta;₂分别是周围山丘的高度和倾斜角度。

在这部分中，我们将考虑一个更为一般的条件，即顶部被击中的锥形山被山地地形包围。图13（a）显示了我们研究中FDTD模型配置的横截面视图。图13（b）示出了相应的三维（3-D）视图，并且锥形山被一连串山丘包围。

图14 在50公里的观测距离处，在闪电辐射的垂直电场上撞击被一连串山丘环绕的锥形山的效果。h₁和h₂分别是锥形山和周围山丘的高度。 假设所有山倾角均为45°，土壤电导率假定为0.01S/m。

图14显示了三种不同情况下距离为50km的雷电辐射垂直电场的对比结果，包括撞击平坦的地面，孤立的锥形山和由一连串山丘环绕的锥形山。假设所有山倾角均为45°（theta;₁=theta;₂=

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[18851]，资料为PDF文档或Word文档，PDF文档可免费转换为Word