定轴齿轮组振动特性分析与仿真研究毕业论文
2020-04-08 14:33:30
摘 要
齿轮传动系统具有结构紧凑,体积小,传动比大,传动效率高等特点,因而广泛应用于汽车,航空,舰船等领域。齿轮传动具有传递效率高,结构紧凑,工作可靠,传动比稳定和恒功率传动的特点,伴随着科技水平的提高,齿轮传动正在向着高速,重载,高精度,高可靠性和自动化的方向发展。其动力学特性的优劣会直接影响设备整机的工作性能。在齿轮系统中,由于时变啮合刚度,齿侧间隙,轴承支承间隙以及制造安装造成的综合啮合误差会导致系统产生剧烈的非线性振动,这种振动会对系统的工作性能及可靠性产生很大影响。本文根据拉格朗日方程,建立了齿轮传动非线性动力学模型,模型中考虑到了齿轮系统的系统阻尼,齿侧间隙等,对动力学方程进行了无量纲化处理,将方程转化为统一的矩阵形式。将矩阵方程转化为控制模型有关的微分方程,利用MATLAB/SIMULINK仿真软件对齿轮间隙非线性动力学模型进行了数值仿真,通过建立合适的仿真程序框图,对影响振动响应特性的参数进行了研究,分析参数变化对系统稳态响应的变化的影响。结果表明,在一定的激励频率区间内,随着激励频率的减小,系统的响应首先由单周期谐振动响应演变为二周期的次谐响应,然后演变为四周期的次谐响应,最后表现为混沌响应;在齿侧间隙一定的情况下,轴承支承间隙加强了系统的非线性。基于SIMULINK数值方法方便求解复杂的齿轮传动系统动态响应,为深入研究齿轮非线性动力学问题提供方法。
关键词: 齿轮;SIMULINK ;数值方法 ;系统非线性
Abstract
The gear transmission system has the characteristics of compact structure, small volume, large transmission ratio and high transmission efficiency, so it is widely used in automobile, aviation, ship and other fields. Gear transmission has the characteristics of high transmission efficiency, compact structure, reliable work, stable transmission ratio and constant power transmission. With the improvement of scientific and technological level, gear transmission is developing in the direction of high speed, heavy load, high precision, high reliability and automation. Its dynamic characteristics will directly affect the performance of the whole machine. In the gear system, due to the time-varying meshing stiffness, the tooth side gap, the bearing support gap and the integrated meshing error caused by the manufacturing and installation, the system produces violent nonlinear vibration. In this paper, the nonlinear dynamic model of gear transmission is established according to the Lagrange equation. In this model, the system damping of the gear system and the gap of the tooth side are taken into consideration, and the dynamic equation is treated without Dimensionalization, and the equation is converted into a unified matrix form. The matrix equation is transformed into a differential equation related to the control model, and the MATLAB/SIMULINK simulation software is used to simulate the nonlinear dynamic model of the gear gap. By establishing a suitable block diagram of the simulation program, the parameters affecting the vibration response characteristics are studied, and the changes of the parameter change to the steady state response of the system are analyzed. The results show that in a certain range of excitation frequency, with the decrease of the excitation frequency, the response of the system evolves from a single periodic harmonic response to a subharmonic response of two cycles, and then turns into a subharmonic response of the four cycle, and the final expression is a chaotic response. When the clearance is fixed, the bearing clearance enhances the nonlinearity of the system. Based on the SIMULINK numerical method, it is easy to solve the complex gear transmission system dynamic response, and provides a method for in-depth study of the nonlinear dynamic problems of gears.
Key words:gear ;Simulink; numerical method ;System nonlinearity
目录
第1章 绪论 6
1.1课题研究背景 6
1.2研究的目的及意义 6
1.3国内外研究现状 7
1.4研究内容及方法 8
1.4.1研究内容 8
1.4.2研究目标 9
1.4.3研究方法 9
第2章 直齿定轴齿轮组动力学模型 10
2.1定轴齿轮组动力学特性规律 10
2.2定轴齿轮组力学公式 10
第3章 软件设计及其结果分析 13
3.1方案分析与确定 13
3.2软件介绍 13
3.3软件程序图的建立 14
3.4软件仿真 16
3.4.1频率对振动特性的影响 16
3.4.2齿轮间隙对振动特性的分析 18
3.5直齿定轴齿轮组振动响应规律小结 19
第4章 总结及后续工作 20
4.1论文总结 20
4.2存在不足及其后续工作 20
参考文献 22
致谢 24
第1章 绪论
1.1课题研究背景
齿轮传动是精密机械中应用最为广泛的传动机构。主要用途是:1.传递任意两轴之间的运动和转矩。2.变换运动的方式,将转动变为移动或将移动变为转动。3.变速—将高转速变为低转速,或者将低转速变为高转速。在机器中一般是用来实现减速,而在仪器仪表中除了用在减速之外,还经常用与增速,来实现传动放大的作用。
和摩擦轮传动和带传动等来比较,齿轮传动比较稳定,精度高;在功率相同情况下,具有尺寸较小,结构紧凑;效率高,寿命长的优点。
齿轮零件在各种机器设备中经常得到利用,在工业发展的进程中发挥了十分重要的作用,工业上的机器构件的工作性能和使用寿命都会受到齿轮精度的影响,此外,齿轮的应用多,范围广,相关的质量检测也越来越受到重视。齿轮形状复杂,涉及到的参数多,各种误差种类繁多,测量难度较大。尽管随着技术的发展,出现了一些智能化齿轮,但是制作的成本高,而且使用和维护需要大量专业知识和技术操作。所以很多商家考虑到成本的原因还是会传动工艺来制作加工齿轮,最常见的加工工艺就是接触式测量。这些工艺存在着很多缺点,例如:工作量大,测量工作时间长。齿轮工作时产生振动造成设备动态性能恶化,振动是反映齿轮传动质量的重要指标,齿轮工作的振动不仅会产生噪声,还会导致系统的不稳定性,严重甚至会造成传动系统失效,出现意外,因此研究齿轮的振动响应特性在实际中有着很大的作用。
本文就是在齿轮振动特性的规律下,进行对定轴直齿齿轮组相关实验,得出振动响应规律,分析多组对照实验的结果,与定轴直齿齿轮组振动响应特性规律进行比照,相互验证,并得出结论。
1.2研究的目的及意义
齿轮传送可以看成为最常见的机械传动形式之一,广泛地应用于机械,电子,采矿,冶金,汽车,航空航天等一些领域。齿轮传动具有传递效率高,结构紧凑,工作可靠,传动比稳定和恒功率传动的特点,伴随着科技水平的提高,齿轮传动正在向着高速,重载,高精度,高可靠性和自动化的方向发展。其动力学特性的优劣会直接影响设备整机的工作性能。可是齿轮传动的结构形式多样、内外部激励和非线性因素丰富,而且工作环境复杂多变,这令其动力学分析相比较于其他机械系统更加复杂。此外,制造、加工、装配等的误差、磨损、润滑和运行环境等因素也将导致齿轮系统的内外部激励和系统参数具有不确定性。齿轮系统动力学分析需要考虑这些不确定性因素。
1.3国内外研究现状
随着非线性动力学理论的发展,齿轮系统的非线性特性成为研究的热点。例如,卡勒曼和辛格以researchefem软件,还有其他等人研究了直齿圆柱齿轮单自由度模型的稳态响应和稳定性,考虑了齿轮误差、时变刚度和阻尼与啮合刚度成正比。同时,用Hill无穷行列式计算分离稳定区域和不稳定区域的缓和曲线。在一系列的论文,theodossiades和natsiavas 研究含间隙的齿轮系统的非线性动力学,周期啮合刚度、静态传动误差和外部激励,这是由扭矩齿轮几何误差引起的。为了说明重要参数对系统响应的影响,采用适当的方法确定了一些类型的响应图。基于有限元/接触力学模型,帕克等人研究了直齿圆柱齿轮在较宽的工作速度和扭矩下的动态响应,证明了二维有限元/接触力学公式能够准确地捕捉齿轮系统的强非线性动力学行为。考虑到触点的实际位置和齿轮的齿的实际变形,安德松和vedmar 提出了一种方法来确定两旋转弹性螺旋齿轮之间的动态负载,并预测齿轮组的动态行为。他们还提出了一些数字来显示动态传输误差的行为以及接触压力的变化。shyyab和卡勒曼开发了一个非线性时变动态模型来研究谐波的一个典型的多网格轮系与混沌运动。文中还描述了系统的交错网格刚度幅值、齿轮啮合阻尼和静力矩传递等系统参数对次谐波运动的影响。增量谐波平衡法(结合)是应用分析单自由度和间隙的齿轮系统的非线性动力学,时变刚度和静态传递误差,混沌响应的数值模拟的方法。
建立了一种考虑时变啮合和侧隙非线性的准双曲面齿轮副广义动力学模型。研究了系统的周期响应、混沌和分岔等非线性现象。此外,提出了具有时变非线性啮合刚度、啮合阻尼和侧隙特性的准双曲面齿轮副系统的非线性时变动力学模型,研究了驱动面和边面啮合刚度不对称对动力响应的影响。研究了一种自由的齿轮系统动态响应单自由度和非线性悬架和发现周期性动态变化的相图,意味着能量谱分析及混沌,Poincaré地图,在这个系统的Lyapunov指数和分形维数。描述了一种用于分析直齿圆柱齿轮传动接触力和脱层的先进模型。通过一个实例的准静态分析验证了模型的正确性,并评估了传递扭矩的大小、摩擦和修正的中心距离对产生的传动误差、啮合刚度和载荷分担比的影响。开发了一个六度的弯曲自由度耦合动力学模型,扭斜齿轮传动系统的运动和轴,其中包括时变啮合刚度、轴承支承刚度、啮合阻尼和间隙。分析了接触比、支承刚度、阻尼以及侧隙等因素对动态传动误差和稳定性的影响。
farshidianfar和Saghafi研究全球一个齿轮非线性系统的混沌行为的过渡采用Melnikov方法。此外,数值分岔分析和数值模拟,包括分岔图,相平面图,时间历程,功率谱,和庞加莱部分被用来确认分析预测,并显示过渡到混乱。建立了三自由度直齿圆柱齿轮传动系统的动力学模型,研究了转矩波动、齿轮阻尼比、齿轮侧隙、啮合频率和啮合刚度等因素对低频激励随机扰动的影响。研究发现,在具有非线性间隙的齿轮系统中,存在着丰富的倍周期分岔现象。为了研究耦合参数变化下的分叉和齿轮系统的混沌特性设计了一种基于简单单元映射法和逃逸时间算法的扭振齿轮系统多状态参数耦合动态状态检测算法。在相空间中的同宿轨道被发现在非光滑系统的周期运动轨迹法研究不同造成的。
在国内,齿轮动力学也被进行了大量研究。在2001年,李润芳等人建立具有误差激励和时变刚度激励的齿轮系统非线性微分方程,利用有限元法求得齿轮的时变啮合刚度和啮合冲击力,研究了齿轮系统在激励作用下的动态响应。在2006年,杨绍普等人研究了考虑时变刚度,齿轮侧隙,啮合阻尼和静态传递误差影响下的直齿轮副的非线性动力学特性,利用增量谐波平衡法对系统方程进行了求解,研究了系统的分岔特性以及阻尼比和外激励大小对系统幅频曲线的影响。在2010年,刘国华等人建立了考虑齿轮轴的弹性、齿侧间隙、油膜挤压刚度和时变啮合刚度等因素的多体弹性非线性动力学模型,研究了齿廓修形和轴的扭转刚度对动力学特性的影响。在2013年,王晓笋,巫世晶等人建立了含有非线性齿侧间隙、内部误差激励和含磨损故障的时变啮合刚度的三自由度齿轮传动系统平移扭转耦合动力学方程。采用变步长GILL积分、GRAM-SCHMIDT方法,得到了系统对应的分岔图和李雅普诺夫指数谱,研究发现了系统内部丰富的非线性现象,而系统进入混沌系统的途径也是多样的。
1.4研究内容及方法
1.4.1研究内容
(1)深入理解齿轮组等典型旋转机械的振动响应规律(2)研究直齿定轴齿轮组动力学模型,总结直齿定轴齿轮组振动特性规律(3)在Matlab/Simulink环境中进行直齿定轴齿轮组动态仿真,设计相关实验,,调试实验参数,得出实验结果,经过仔细分析,验证直齿定轴齿轮组动力学模型。
1.4.2研究目标
在Matlab/Simulink环境中进行直齿定轴齿轮组动态仿真,设计相关实验,验证直齿定轴齿轮组动力学模型。在元件库中调取齿轮相关的结构元件,搭建模块框图,处理模块连接,设置参数,进行动态仿真,验证直齿齿轮组动力学模型,分析振动响应的规律,观察实验结果是否和理论上的结果相符,最后进行小结。
1.4.3研究方法
首先分析直齿定轴齿轮的动力学公式,列出相关的力学方程式,引入无量纲量,将力学方程转化为矩阵方程,再将矩阵方程化为微分方程,学习并且运用Simulink软件来进行对定轴齿轮组的仿真研究,在构建好合适的正确的程序图后,设置好模块的参数变量,根据齿轮的振动振幅特性因素的影响原因,改变这些变量来得出这些因素对结果的影响,通过调试相关因素的参数,设立对照实验,输出图示等结果,分析单次实验的结论,然后进行多次实验,得出多组实验结果,分析每次实验的结论,并且进行比较,得出合适的结论
第2章 直齿定轴齿轮组动力学模型
2.1定轴齿轮组动力学特性规律
当齿轮系运转时,若其中各齿轮的轴线相对于机架的位置都是固定不变的,则该齿轮系称为定轴齿轮系。直齿定轴齿轮组的运动特性有:通过进行改变齿轮转速即频率,我们根据相平面图上图形的形状,可以知道系统齿轮的频率在一定的范围内减小会导致复杂非线性振动变化,齿轮振动响应是由单周期性变成多周期,并且最终演变为混沌响应。而当频率一定时候,间隙越小,齿轮的系统振动响应越显线性,在啮合间隙一定的情况下,主动轮轴承支承间隙和从动轮轴承支承间隙增强齿轮系统的非线性。
2.2定轴齿轮组力学公式
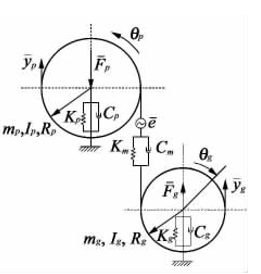
图2.1直齿圆柱齿轮组传动模型
此次讨论的是不考虑齿面摩擦情况下,典型的直齿圆柱齿轮组动力学模型,如图2.1所示,系统可以看作是拥有四个自由度的齿轮组传动系统,分别是旋转自由度和平移自由度。
在图中,主动轮和从动轮分别用下标p,g表示,代表的是齿轮传递的静态误差,会随时间变化,是主动轮的扭转位移,是从动轮的扭转位移,是主动轮的振动位移,是从动轮的振动位移,是扭转振动从而引起的主动轮和从动轮在啮合线方向产生的相对位移,也会随时间变化,有=-,其中对应的是主动轮的基圆半径,对应的是从动轮的基圆半径;是主动轮平移质量,是从动轮的平移质量,是扭矩等效质量,且有=,其中是主动轮的转动惯量,是从动轮的转动惯量;是主动轮的支承阻尼系数,是从动轮的支承阻尼系数,是啮合阻尼系数;是主动轮的轴承支承间隙,是从动轮的轴承支承间隙,是啮合间隙;是主动轮的支承刚度系数,是从动轮的支承刚度系数,是啮合刚度系数;、、分别是对应的间隙非线性函数;是作用在主动轮上的动态啮合力,是作用在从动轮上的动态啮合力;(t)是由激励转矩的平均分量引起的齿轮啮合力,(t)是由激励转矩的交变分量引起的齿轮啮合力。令动态啮合误差和静态传递误差的差值为(t),则
()=() ()-()-()(1)
对于这个齿轮系统有:
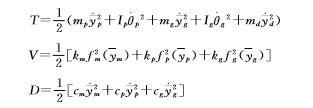 (2)
(2)
由拉格朗日方程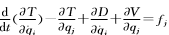 得到系统的非线性动力学方程为:
得到系统的非线性动力学方程为:
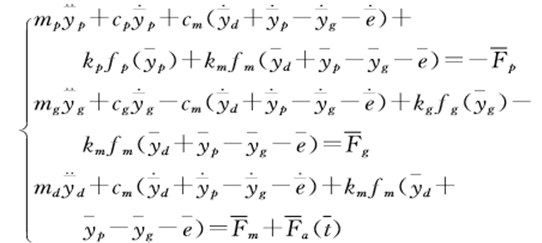 (3)
(3)




