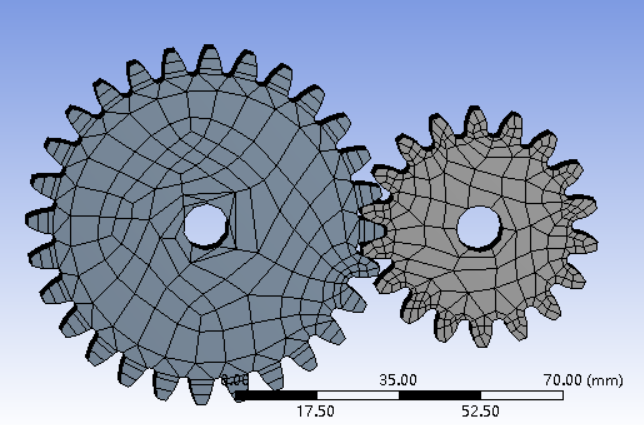
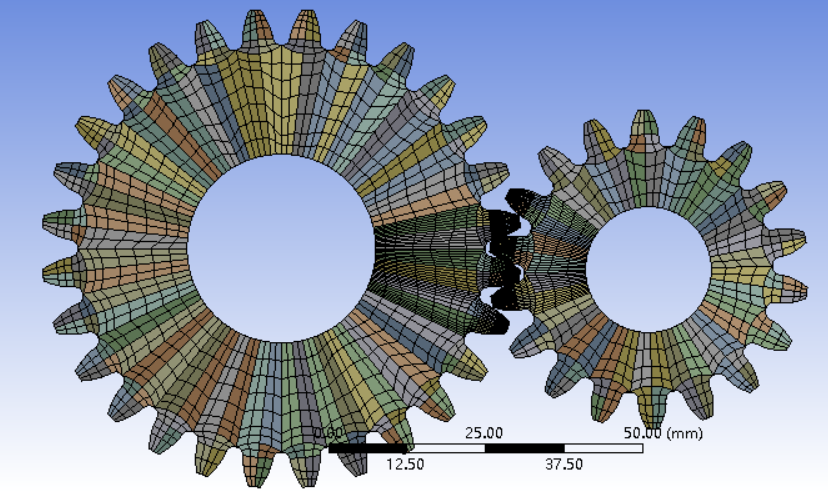
齿轮组啮合过程仿真分析毕业论文
2020-04-08 14:33:22
摘 要
齿轮是动力传动系统中最重要的部件,当齿轮单双齿交替啮合时,由轮齿弹性变形引起的刚度激励会使齿轮产生振动和噪声,因而确定啮合轮齿的啮合刚度一直是齿轮动力学的重要任务。啮合刚度是齿轮啮合时轮齿抵抗变形的能力。在齿轮刚度(弹性)范围内,啮合刚度是齿轮所受载荷与位移成正比的比例系数,即引起单位位移所需的力。随着科技的飞速发展,越来越多的计算机技术应用与齿轮的分析中,而有限元法是基于近代计算机的快速发展而发展起来的一种近似数值方法, 用来解决力学,数学中的带有特定边界条件的偏微分方程问题。传动齿轮复杂的应力分布情况和变形机理是造成齿轮设计困难的主要原因,而有限元理论和各种有限元分析软件的出现,让研究人员无需对齿轮受力做大量的计算和研究,就可以基本掌握齿轮的受力和变形情况,并可利用有限元计算结果来计算齿轮特性,从而更好的对齿轮进行分析。
在本次毕业设计中,根据齿轮的几何参数在solidwork中建立齿轮的三维建模仿真并装配为齿轮组,为更好的对模型进行有限元分析,因此对模型进行分割;将模型导入ansys workbench中后使用静态动力学模块对三维模型进行有限元分析,添加材料,设置接触对,进行网格划分与细化,施加约束,建立有限元接触模型,模拟齿轮传动状态,计算齿轮的啮合刚度,使用齿轮啮合基本公式验算;计算单双啮合区间,通过旋转齿轮改变其接触位置,分别导入到workbench中对其进行有限元分析,计算出齿轮在不同状态下的啮合刚度并分析其周期性变化规律。
关键词:三维建模;网格划分;有限元分析;啮合刚度
Abstract
Gear is the most important part in the power transmission system. When the single and double gear teeth are engaged, the stiffness excitation caused by the elastic deformation of the gear will cause the gear to produce vibration and noise, so it is an important task of the gear dynamics to determine the meshing stiffness of the meshing tooth. In the range of gear stiffness (elasticity), mesh stiffness is proportional to the load and displacement of gear, that is, the force required for unit displacement. With the rapid development of science and technology, more and more computer technology applications and gear analysis, and finite element method is an approximate numerical method based on the rapid development of modern computer, which is used to solve the problem of partial differential equations with specific boundary conditions in mechanics and mathematics. The complicated stress distribution and deformation mechanism of the transmission gear are the main reasons for the difficulty in the gear design, while the finite element theory and the appearance of various finite element analysis software make the researchers do not need to do a lot of calculation and Research on the force of the gear, so that the force and deformation of the gear can be basically mastered, and the finite element can be used to make use of the finite element. The results of the meta computation are used to calculate the gear characteristics so as to better analyze the gears.
In this graduation design, the 3D modeling and Simulation of gear is built in SOLIDWORK based on the geometric parameters of the gear and the gear group is assembled. In order to make the finite element analysis of the model better, the model is segmented, and the model is introduced into the ANSYS Workbench to use the static dynamic module to carry out the finite element analysis of the three-dimensional model. Analysis, adding material, setting contact pair, dividing and refining grid, applying constraint, establishing finite element contact model, simulating gear transmission state, calculating gear meshing stiffness, checking calculation of gear meshing basic formula, calculating single and double meshing interval, changing its contact position through rotating gear, importing to workb The finite element analysis is carried out in ench, and the meshing stiffness of gears under different conditions is calculated, and the periodic change rules are analyzed.
Key words: 3D modeling; mesh generation; finite element analysis; meshing stiffness.
目 录
1.绪论 1
1.1课题背景及研究意义 1
1.2国内外的研究现状 1
1.3本文研究的工作 2
2.齿轮参数与刚度公式 2
2.1齿轮参数 2
2.2齿轮啮合刚度公式 3
3.直齿轮三维建模 4
3.1齿轮建模方案 4
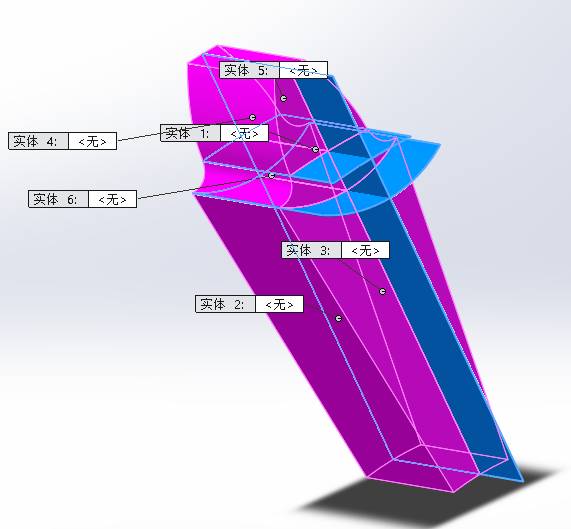
3.2模型优化 5
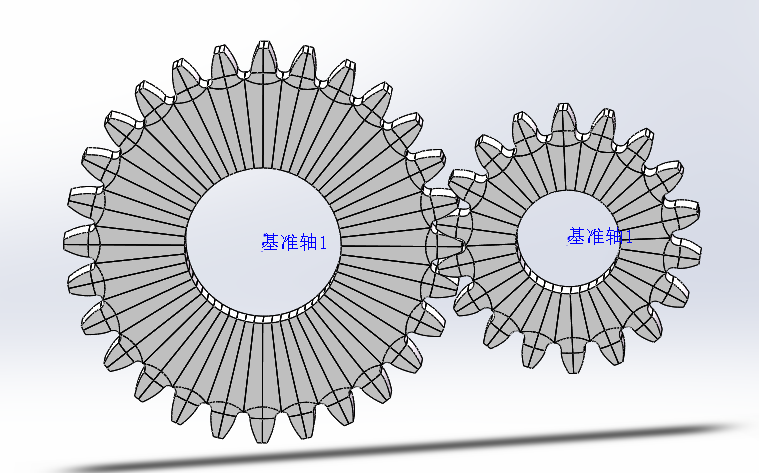
3.3模型装配 6
3.4模型导入 7
4.齿轮啮合刚度计算 7
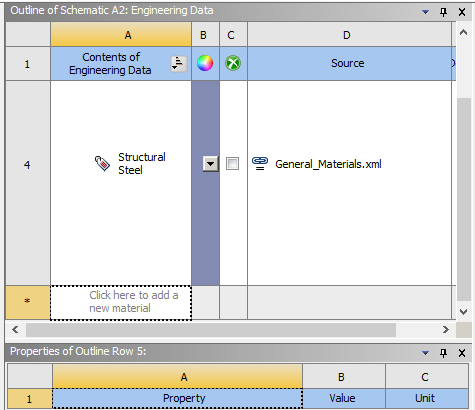
4.1导入材料与网格划分 8
4.2创建接触与施加约束 10
4.3仿真求解 11
4.4仿真结果验算 13
5.啮合刚度周期变化规律 14
5.1啮合位置的确定 14
5.2齿轮啮合刚度变化 16
5.3刚度变化规律 16
6.总结及后续工作 17
6.1论文总结 17
6.2存在的不足与后续工作 18
参考文献 19
致谢 21
1.绪论
1.1课题背景及研究意义
齿轮是旋转机械中最关键的部件之一,已有着上千年的历史。他由于具有瞬时传动比恒定、工作平稳、传动准确可靠等特点,有着其他传动不可替代的优势,在各个机械领域都发挥出巨大的作用。因此对于齿轮而言,其设计与制作水平将会对齿轮与机械的性能和质量产生直接的影响。而随着科技的飞速发展,越来越多的计算机技术应用于齿轮的设计与制作中,对齿轮的分析也在不断的应用着当代前沿科学理论和方法。依靠计算机与软件技术,我们可以更有效的对齿轮进行仿真分析,得到齿轮的各种情况下的状态,用以得出更好的实际齿轮难以做到的结论。
如今仅仅只研究齿轮的齿廓修形、螺旋角修形早已不能满足人们对于机械性能的要求,齿轮的更多特性:如齿轮的振动、强度及刚度引起了越来越多的学者关注并对其进行分析。在齿轮啮合过程中,齿轮并不是理想刚体,在载荷作用下,轮轴与轮齿均会发生不同程度的弹性变形,使传动系统中的输入轴转速超前于输出轴。而且当齿轮负载迅速改变时,输出转角可能不会与输入转角完全同步,并且将会产生振动。虽然这种误差可能十分微小,在大多数的场合下可以忽略,但当其发生在精密仪器仪表时,一个微小的误差可能也会被放大到不能忽视,影响到最终结果。齿轮啮合时轮齿抵抗变形的能力正是齿轮啮合刚度,因此齿轮啮合刚度也是齿轮的重要参数之一。对啮合刚度进行研究可以降低齿轮的噪声和振动,减小齿轮在传动误差,所以齿轮的啮合刚度的研究也就显得尤为重要。
1.2国内外的研究现状
如今对直齿圆柱齿轮动态模型的研究已经有进行大量的研究,许多的学者对齿轮啮合刚度奉献了自己一份力。目前啮合刚度共有两种计算方法:一种为理论计算方法,它包括保角映射法和材料力学方法;另一种则是数值计算方法,它包含有限元法、边界元法和回归法,其中最常见也是最常用的一种方法是有限元法。
保角映射法是弹性力学的一种解析解法,对于给定受力形状的边界曲线可以得到精确的解。首先将这一力学方法引入齿轮的力学分析是由寺内喜男和会田俊夫等人做出的。保角映射法能很精确地表达齿形和齿根过度曲线。保角映射法本质上是将齿轮曲线边界映射为直线边界,然后通过复变函数求解出位移场,从而得到齿轮负荷处的应力与变形。
材料力学方法是一种最早使用且使用较为广泛的齿轮啮合刚度计算方法。一般其方法是将齿轮轮齿简化成弹性基础上的变截面悬臂梁来计算齿轮轮齿变形,材料力学方法认为啮合齿轮的总变形由悬臂梁的弯曲变形和剪切变形、基础的弹性变形导致的附加变形及轮齿接触部分变形等三部分组成。材料力学方法计算齿轮啮合刚度时为了简化计算,对齿轮模型需进行适当的简化,根据齿轮模型的不同简化方式,有各种不同的计算方法。其中较为有名的是石川公式和Weber-Bannaschck计算公式。石川公式在日本有着广泛应用,在计算啮合刚度时,石川公式将轮齿简化成矩形与梯形,通过分别计算矩形与梯形的弯曲变形,剪切变形与基础部分形变量来求得接触点沿啮合线的位移。而Weber-Bannaschck公式是计算齿轮变形的权威方法之一,在解决实际问题中应用较为广泛。因为此种算法并没有简化轮齿的齿廓,而是将齿廓看为渐开线,所有其求得的误差也比较小。
随着科技的发展,数值计算方法不论是从精度上来说,还是从经济效益来说,都有着质的飞跃,应用的范围也越来越广泛。数值计算方法计算齿轮啮合刚度由许多种方法,但有限元法是最常用。有限元的核心思想是将复杂的三维模型离散划分为有限个单元,将理想化的假定与力学控制施加于每个单元上,对每个单元进行分析后组装为总的结构变化。所以单元的划分本应越小越好,当然并非是划分的单元越小越好,过小的单元划分会导致数值计算上的误差放大。同时虽然有限元的理论早已提出但当时并没有那么大计算量的工具,正是随着科技的发展,有限元理论才得以发挥它的光芒。早在20世纪70年代,有限元分析已在各个领域被广泛的应用,学者们开始使用有限元来求解各种复杂的实际问题。而齿轮也是其中的一个研究对象。而如今有着各种各样的有限元分析软件供我们使用,如ANSYS、UG等甚至连SolidWorks这种专门用于三维建模的软件也可以进行简单的有限元分析,这样正是得益于科技的发展。若要用有限元计算齿轮啮合刚度,需要先建立齿轮的三维模型,再导入材料,设置接触对与约束条件,进行网格的划分与轮齿的细化,最后求得接触点沿啮合线的形变量,由此来计算出齿轮的啮合刚度。
1.3本文研究的工作
人们对齿轮进行过大量的研究,但大部分是关于齿轮的接触应力、变形载荷等方面,但是很少涉及齿轮变形的影响,如齿轮的强度、刚度及传动误差等。本次研究采用有限元来对齿轮的啮合过程进行研究。具体方案为使用Geartrax插件在SolidWorks建立齿轮的三维模型,提取出齿轮齿廓对其进行二次建模与分析,然后装配两个齿轮。将装配体模型导入到ANSYS中,使用静态动力学模块对模型进行有限元分析。将齿轮的啮合过程分为不同的状态来分析这样既可以比较直观的观察啮合时齿轮的状态,同时可以预防动态时齿轮运动产生的误差。
2.齿轮参数与刚度公式
2.1齿轮参数
此次研究的直齿轮齿廓为渐开线,被称之为渐开线直齿轮,具有能保持恒定的传送比,角速不变的优点。若要对此类齿轮进行三维建模,关键就是要生成正确的渐开线。齿廓的渐开线的可以看为一条直线沿着基圆作无摩擦滚动时直线上某一固定点的运动轨迹。关键就是要生成正确的渐开线。由《精密机械原理》可知,渐开线方程为:
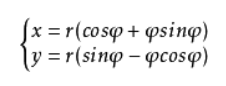 (1)
(1)
其中r为基圆半径, ψ为固定点与基圆圆心连线和X轴之间的夹角。
有时需要测得压力角求齿轮啮合刚度,为此需要了解齿轮压力角的定义。压力角是当无摩擦的情况下,接触点法向压力的方向线与该点啮合线方向的交角。下图为齿轮压力角:
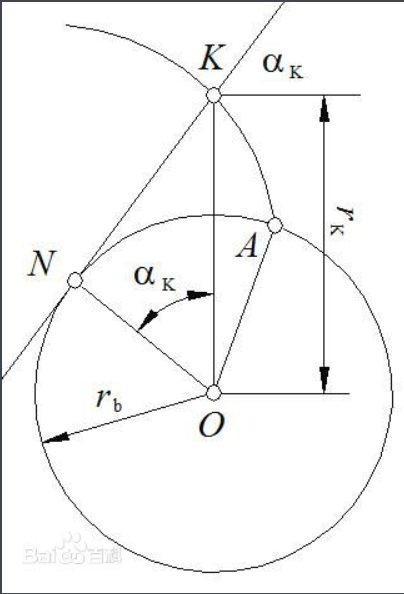
图2.1齿轮压力角
其中αk为齿轮压力角,NK为齿轮啮合线。由αk=arccos(KO/NA)可以从图2.1看出渐开线上每个点的压力角是不同的,离基圆越远,压力角越大。基圆上的压力角为0,这里设置分度圆上的压力角为20度。
2.2齿轮啮合刚度公式
当齿轮的重合度大于1时齿轮在一个啮合周期内有两次变化,从双啮合区间到单啮合区间再到双啮合区间。双啮合区间是主动轮有两个轮齿同时与从动轮接触,单啮合区间是主动轮只有一个轮齿与从动轮接触。在齿轮的啮合过程中,每一对齿轮都可以看成是一个弹簧连接,啮合刚度在一个弹簧连接和两个弹簧连接之间变化,因此在一对啮合周期内齿轮啮合刚度会发生两次阶跃性的变化。由此可以猜测齿轮的啮合刚度的变化规律是一对齿轮接触的啮合刚度明显大于两对齿轮接触的啮合刚度。
刚度的定义是抵抗弹性变形的能力,而齿轮啮合刚度的基本定义为:
 (2)
(2)
其中,δ为沿啮合线的形变量,为啮合点的法向里,B为齿轮齿宽。
但是通过有限元分析直接求解接触点沿啮合线的位移非常困难,因此根据参考文献中Sirichai所提出的概念,齿轮的扭转刚度是输入扭转载荷与齿轮总角转动的比值。总角转动定义为齿轮在固定啮合齿轮中啮合时由于齿轮齿的弯曲而转动的角度。其可以通过齿轮体总的弹性旋转角度可以求出齿轮接触点沿啮合线的位移:δ=Δθrb,其中的rb为主动轮基圆半径,Δθ为齿轮的体总的弹性旋转角度同时也是基圆转动角。由=T/rb可将齿轮啮合基本公式转换为:
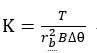 (3)
(3)
其中T为齿轮的负载转矩。
从公式可以看出啮合齿轮刚度与负载转矩成正比,与基圆转角成反比。而本次毕业设计中转矩是分析时设置的且固定不变,所以只需求出齿轮的基圆转角即可算出齿轮啮合刚度,大幅度降低了计算量。
3.直齿轮三维建模
研究齿轮的啮合过程,最开始同时最关键的一步就是对齿轮进行三维建模,由于在workbench中建模较为繁琐且支持三维软件模型导入,所以这里使用SolidWorks进行齿轮的三维建模。SolidWorks是由美国SolidWorks公司推出的功能强大的三维机械设计软件系统,有这功能强大、易学易用和技术创新三大特点,这使得SolidWorks 成为领先的、主流的三维CAD软件。齿轮模型的精确度将会影响到接下来的有限元分析。使用SolidWorks对齿轮进行三维建模,可以使模型更易建立并且更加准确。
齿轮组参数如下表所示:
模数m/mm | 压力角α/° | 大齿轮齿数z1 | 小齿轮齿数z2 | 齿宽b/mm |
2.54 | 20 | 28 | 18 | 10 |
根据精密机械设计中的标准直齿轮几何尺寸计算公式,可以得到齿轮高ha=m=2.54mm,齿根高hf=1.25m=3.175mm,大齿轮分度圆直径d1=mz1=71.12mm,小齿轮分度圆直径d2=mz2=45.72mm。
3.1齿轮建模方案
在SolidWorks中常用的齿轮建模方案有三种:1、已知参数使用方程式建模;2、用toolbox标准库建模;3、使用geartarx插件建模。齿轮仿真时,精确的渐开线和是齿轮建模的关键。
方案一使用SolidWorks中的工具中的方程式建立轮齿齿廓的渐开线方程,使用第二章渐开线齿轮齿廓的方程即可画出齿轮渐开线。其中rb=db/2为基圆半径,为渐开线走过的角度,设置为0~π即可。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: