摘 要

无损压缩是一种降低数据量，获得低字节流的数据表示，但没有丢失任何数据的压缩方式。随着对数据无损压缩的效率和实时性的要求越来越高，快速的数据无损压缩技术和算法的研究势在必行。本文介绍了开发一个无损压缩程序的设计与实现过程，主要从研究无损压缩算法方面来进行无损压缩方法的研究，通过选取典型的无损压缩算法来对这些算法的特点进行了解并进行算法的实现，选取了基于先验知识的哈夫曼算法和基于自适应字典模型的LZ77算法来实现无损压缩，使用JAVA语言来实现哈夫曼算法和LZ77算法，通过Swing程序设计来设计界面，以直观显示两种无损压缩算法的压缩比和压缩时长，实现了无损压缩的功能。

在分析了各种无损压缩算法的特点的基础上，选取了两种典型的无损压缩算法：哈夫曼算法，LZ77算法。介绍了开发无损压缩程序所用到的技术，主要介绍了JAVA Swing程序设计，哈夫曼算法的原理和LZ77的算法原理；本文按照软件工程的描述方法，详细介绍了整个系统的实现过程；在此基础之上给出了系统实现时若干核心特性的实现手段，并从软件测试的角度出发，以无损压缩系统的测试为例，给出了对一个软件系统进行测试的方法，并得出了测试结论。全面总结了整个系统的设计与实现所采用的技术与软件工程方法，并给出了下一步的研究方向。

本文研究内容以实现无损压缩为目标，较全面地完成了整个无损压缩系统的开发，为以后无损压缩的研究提供了一定的借鉴意义。

关键词：无损压缩；哈夫曼算法；LZ77算法；JAVA

Abstract

Lossless compression is a way to reduce the amount of data, obtain a low byte stream of data representation, but without any loss of data compression. With the increasing demand for the efficiency and real-time performance of lossless data compression, it is imperative to study the fast data lossless compression techniques and algorithms. This article introduces the design and implementation of a lossless compression program. It mainly studies the lossless compression methods from lossless compression algorithms, and selects typical lossless compression algorithms to understand the characteristics of these algorithms and implement the algorithm. The Huffman algorithm based on prior knowledge and LZ77 algorithm based on adaptive dictionary model are chosen to achieve lossless compression. The Huffman algorithm and LZ77 algorithm are implemented using JAVA language. The interface is designed through Swing program design to display two visually. The lossless compression algorithm's compression ratio and compression time enable lossless compression.

On the basis of analyzing the characteristics of various lossless compression algorithms, two typical lossless compression algorithms are selected: Huffman algorithm and LZ77 algorithm. The techniques used in the development of lossless compression programs are introduced. The JAVA Swing program design, the principle of Huffman algorithm and the algorithm principle of LZ77 are introduced. This paper describes the implementation process of the whole system in detail according to the description method of software engineering. On the basis of the above, the realization means of several core features in the implementation of the system are given. From the perspective of software testing, the test of a lossless compression system is given as an example, and a method of testing a software system is given and a test is obtained. in conclusion. A comprehensive summary of the design and implementation of the entire system used by the technology and software engineering methods, and gives the next research direction.

This article studies the content to realize the lossless compression as the goal, completes the development of the entire lossless compression system in a more comprehensive way, provides the certain reference significance for the future lossless compression research.

Key Words：Lossless compression；Huffman algorithm；LZ77 algorithm；JAVA

目录

第1章 绪论 1

1.1 研究的背景、目的及意义 1

1.2 国内外研究现状 2

1.3 主要研究内容 3

第2章 主要技术分析 4

2.1 系统的技术需求 4

2.2 JAVA SWING程序设计 4

2.3 哈夫曼算法 5

2.4 LZ77算法 6

2.5 本章小结 7

第3章 系统分析与设计 8

3.1 系统的需求分析 8

3.2 系统的总体设计 8

3.2.1 系统的主要模块 8

3.2.2 系统的界面设计 9

3.2.3 系统的接口设计 9

3.3 系统的模块设计 11

3.3.1 哈夫曼模块 11

3.3.2 LZ77模块 13

3.4 本章小结 13

第4章 无损压缩程序的实现 14

4.1 系统的界面实现 14

4.2 哈夫曼算法的实现 16

4.3 LZ77算法的实现 19

4.4 测试环境 21

4.4.1 计算机配置 21

4.4.2 存储设备配置 21

4.5 测试 21

4.5.1 哈夫曼压缩解压测试 21

4.5.2 LZ77压缩解压测试 22

4.6 本章小结 23

第5章 总结与展望 24

5.1 总结 24

5.2 个人展望 24

参考文献 25

致谢 26

第1章 绪论

1.1 研究的背景、目的及意义

在互联网时代，在数据通信传送和下载中，媒体数据 （包括视频媒体和音频媒体等）采用数字化的格式，大量的数据资源给存储器的存储容量、通信信道带宽和计算机处理速度带来很大的负担，但因当前科学技术发展有限，很多硬件技术还无法完全满足计算机存储资源的需求，与带宽之间差距还很大，仅靠通过增加存储容量、扩充信道 容量以及提高计算机处理速度等方法来解决这个问题还有一定难度，这就需要考虑压缩。^[1]

数据压缩在信息迅速增长的时代显得越来越重要,信息在存储、传输等过程经常需要压缩。^[2]

自从1948年Oliver提出PCM 理论至今，编码方法已有上百种之多，但大致分为两类：一类是无损编码，另一类是有损编码。^[3]

无损压缩使用数据的统计冗余进行压缩，对经无损压缩后的文件进行解压可以完全恢复原始数据。但是，无损压缩的压缩率受到限制，通常为2：1到5：1。 无损压缩的应用十分广泛，程序、文本数据和特殊应用场合的图像数据（例如指纹图像，医学图像等）均可使用无损压缩来进行数据压缩。

1952 年，Huffman 编码被麻省理工的一名学生提出，哈夫曼编码因其特性后来被用作一种无损压缩格式，并被广泛应用于数据压缩领域。这些年来，霍夫曼码作为一种非常有效的技术被广泛用作图像压缩。^[4]

虽然Huffman编码作为一种广泛并且有效的无损压缩编码，但是它也具备一些弱点。20世纪80年代，数学家们不满足于Huffman编码中的某些致命弱点，他们从新的角度入手，遵循Huffman编码的主导思想，设计出另一种更为精确，更能接近信息论中“熵”极限的编码方法——算术编码。^[5]

20世纪80年代和90年代，两名犹太人Lempel 和Ziv 提出 LZ 字典编码算法。他们提出的LZ系列字典编码算法包括LZ77，LZ78和LZW，LZ字典编码算法压缩效果好、速度快、实现方式相对简单，后来的各种字典编码算法也多是基于这3 种字典编码算法。

无损压缩具备许多优点，比如没有任何数据丢失；用来存储音频时，音频的音质不会受损，并且不受信号源的影响；无损压缩格式可以很方便地进行转换。当然无损压缩仍然存在不足之处，除了压缩比不高以外，还占用空间大，缺乏硬件的支持。

虽然还存在着一定的不足，但是无损压缩的前景毫无疑问是非常光明的，我们可以从存在的无损压缩格式种类之多推断出这一点。随着时代的发展进步，限制无损格式的种种因素将逐渐消失。如硬盘容量的不断扩大，机械硬盘1TB已经成为主流，固态硬盘200GB也在不久后普及，无损格式占用空间大的问题将被解决。并且随着科技的进步，速度更快的解码芯片也会被研发出来，笔者相信将来越来越多的硬盘随身听能够支持无损格式。甚至在不久的将来，闪存随身听的容量都会大幅度提升。现如今人们对高音质的追求越来越甚，无损压缩格式必定会大火。

无损压缩主要用于需要做进一步数据处理，重复地压缩和解压缩以及数据采集昂贵（如指纹图像，遥感图像和医学图像处理）的一些领域。随着对数据无损压缩的效率和实时性的要求越来越高，快速的数据无损压缩技术和算法的研究势在必行。

1.2 国内外研究现状

图像压缩编码的理论和实验研究距今已有近六十年的历史,从理论到实现许多压缩编码技术都被进行了深入的研究。图像无损压缩是指在没有任何图像损失的前提下,降低数据量,获得低比特流的图像数据表示。^[6]无损压缩算法在以前仅仅基于熵编码，经过几十年的发展，无损压缩已经发展到基于一定的模型解相关的熵编码了。虽然各种各样的压缩算法很多，但是它们的主要区别仅仅在于解相关所采用的模型不同。

随着医疗数字化的深入，特别是基于计算机网络的图像存储与传输系统和远程放射学逐渐发展并变得切实可行，这必将对存储设备的容量和网络带宽带来新的挑战，而一些无损压缩方法已经不能满足发展的需要。因此有必要对现有的压缩方法进行改进，以获得算法简单、硬件实现简单的无损压缩方法。同时，必须加紧对新的、更高效的压缩算法的研究，来适应应用的需要。例如，图像表示模型的突破可能会导致无损压缩的质的飞跃。另外，如果脑科学的发展使我们对大脑视觉领域中图像信息处理的机制有了更深入的了解，肯定会促使无损压缩方法迅猛发展，但这些工作在短期内是不可能突破的。

对于高分辨率的医用图像和渐渐出现的高维 (三维、四维 )图像的压缩方法需要进一步的研究。由于高分辨率和高维图像分其内部所存在比普通图像更多的冗余信息，因此如何针对高分辨率和高维图像来设计压缩方法来对它们进行有效压缩是极具有挑战性的。

对于诸如图像数据库的应用程序，不仅仅需要减少其存储的数据量，而且要进行图像数据查询和特征提取。图数据模型,简称图数据,是表示实体和实体间联系的数据模型。^[7]如果可以直接在压缩数据流上进行查询和处理，系统整体性能将会大大提高。 因此新的无损编码方法应该能够查询和处理图像数据。

哈夫曼（Huffman）树,又称最优树是带权路径长度最小的二叉树。^[8]哈夫曼树早已被用于汉字字形的压缩存储。汉字的数量、字体、字号众多，形体复杂，故需要大量的存储空间来存放汉字字形。^[9]因而对汉字字形进行压缩存储应运而生，对汉字字形的压缩可以分为可逆式和非可逆式压缩两大类，这和无损压缩与有损压缩本质上是相对应的只是术语不同而已，哈夫曼压缩属于可逆式压缩，它的压缩率比非可逆式压缩略低，但它最大的优点是还原的字形美观、不失真 。哈夫曼压缩由于其自身的特性，已经被用于实现小点阵汉字库的压缩。小点阵汉字库一般指16×16、24×24点阵的汉字库。^[10]

1.3 主要研究内容

无损压缩程序的设计与实现是本文的主要内容，下面主要从实现的功能和实现的技术手段两个角度上给出文章的研究成果。

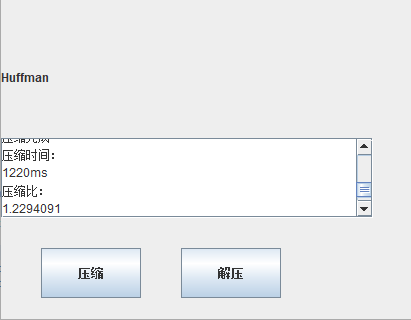
本程序在功能上主要使用哈夫曼算法和LZ77算法实现文件的压缩与解压缩，并显示出压缩比与压缩时长。

本文设计和实现的程序具备以下技术特点：

1. 使用JAVA中的SWING程序设计，实现了该软件的一个简易的见面，主要分为两大模块，哈夫曼与LZ77模块，方便进行对比，并将哈夫曼和LZ77的压缩比和压缩时长分别显示在两大模块中，直观显示便于比较。
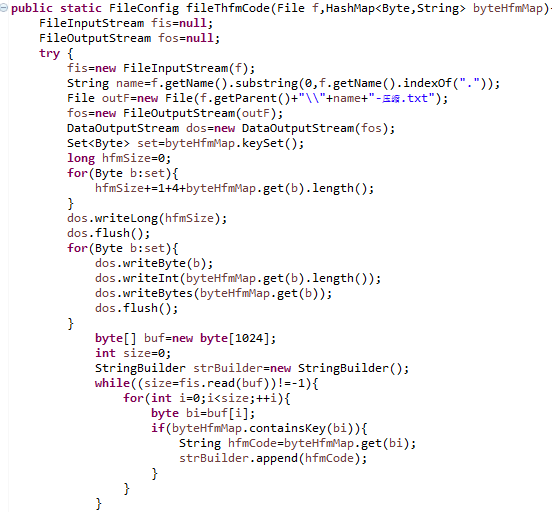
2. 将哈夫曼压缩的压缩信息保存在FileConfig类中，方便解压的时候提取，压缩文件路径和字节对应的哈夫曼编码。

第2章 主要技术分析

2.1 系统的技术需求

在实现压缩程序的技术角度上，文章主要阐述了实现压缩程序所采用的JAVA SWING程序设计，哈夫曼算法和LZ77算法。

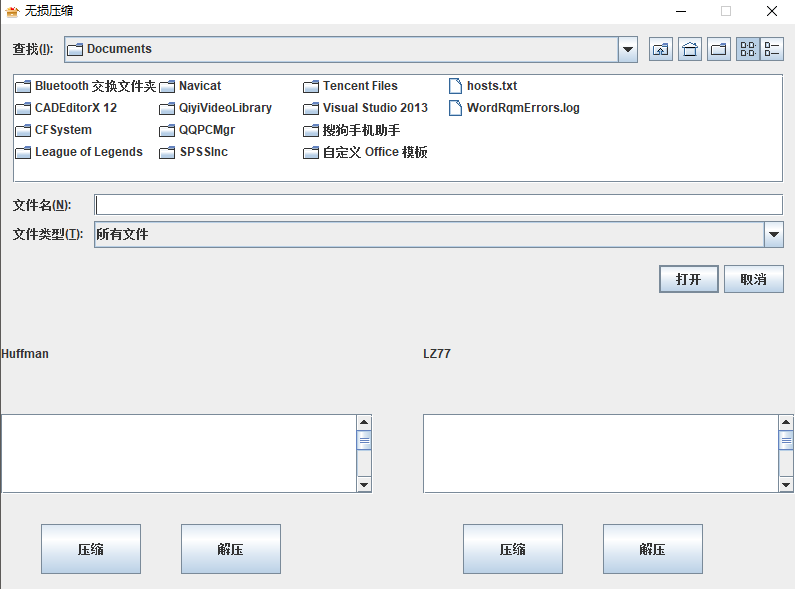
无损压缩的压缩成果笔者想要直观的呈现给程序使用者，因而笔者采用JAVA SWING程序设计为压缩程序设计了一个简要的界面，并且提供了文件选择的组件，方便获取源文件，同时提供了压缩与解压的按钮，实现压缩与解压的功能，并且还提供了两个文本域组件，分别用于显示哈夫曼算法和LZ77算法的压缩比及压缩时长。

哈夫曼压缩属于无损压缩，因而笔者决定使用哈夫曼算法来实现无损压缩，哈夫曼编码是一种基于统计数据的变长编码，得到的编码是一种前缀编码，是一种典型的编码方式，哈夫曼解压缩可完全恢复原始数据。

LZ77压缩也属于无损压缩，LZ77编码是基于字典的编码，它与哈夫曼编码有着很大的不同，因而笔者使用LZ77算法作为另外一种典型的实现无损压缩的压缩算法，在LZ77编码中，主要是输出一个三元组，来对重复的字符串进行编码，LZ77解压缩也可以完全恢复原始数据。

2.2 JAVA SWING程序设计

Swing是一个开发工具包，可以用于开发用户界面。Swing具有丰富、灵活的功能和模块化组件，可以大大简化开发人员开发出一个优雅、美观的用户界面的工作。Swing以AWT为基础，AWT也是Java的一个包，全称是抽象窗口工具包。

工具包中所有的包都是以swing作为名称，例如javax.swing,javax.swing.event
用Swing创建图形界面步骤：
（1）导入Swing包
（2）选择界面风格
（3）设置顶层容器
（4）设置按钮和标签
（5）将组件放到容器上
（6）为组件增加边框
（7）处理事件
（8）辅助技术支持

2.3 哈夫曼算法

哈夫曼算法的原理如下：

假设有k个权值， k个权值分别设为 f1、f2、…、fn，则哈夫曼树的构造步骤如下：

(1) 将f1、f2、…，fn看成是有k棵树，每棵树仅有一个结点，这些树构成森林；

(2) 在森林中选出两个根结点的权值最小的树，将这两棵树作为一棵新树的左、右子树，并且新树的根结点权值为这两棵子树根结点权值之和；

(3)从森林中删除选取的两棵树，并将新树加入森林；

(4)重复(2)、(3)步，直到森林中只剩一棵树为止，该树即为所求得的哈夫曼树。

霍夫曼树是一棵二叉树，它代表给定字母表中与其字符频率分布有关的最有效的二进制码。^[11]

在数据通信中，需要将传送的文字转换成二进制的字符串，用0，1码的不同排列来表示字符。传送报文时其总长度越短越好，一般说来，报文中各个字符的出现频度或使用次数是不相同的，自然而然会想到设计编码时，让使用频率高的用短编码，使用频率低的用长编码，来优化整个报文编码。

使用不等长的编码又会带来新的问题，即不等长编码必须为前缀编码，即要求一个字符的编码不能是另一个字符编码的前缀。为使不等长编码为前缀编码，可用字符集中的每个字符作为叶子结点生成一棵编码二叉树，因为所有字符均为叶子节点，所以编码必为前缀编码，另外为了获得传送报文的最短长度，可以将每个字符的出现频率作为字符结点的权值赋予该结点上，显然字符使用频率越小权值越小，权值越小就越偏离根结点；字符使用频率越大权值就越大，权值越大越靠近根结点。于是频率小编码长，频率高编码短，这样就保证了此树的最小带权路径长度效果上就是传送报文的最短长度。因此，求传送报文的最短长度问题转化为求由字符集中的所有字符作为叶子结点，由字符出现频率作为其权值所产生的哈夫曼树的问题。利用哈夫曼树来设计二进制的前缀编码，既满足前缀编码的条件，又保证报文编码总长最短。

2.4 LZ77算法

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：