摘 要

在我国辽阔的疆域范围内，分布着众多河流。丰富的水资源为交通带来了便利，但如果发生堤坝溃决事故，也会沿岸人民生命财产带来巨大的损失。因此如何准确的预测溃坝波影响范围，具有重要的现实意义。

本文基于fluent软件，采用Standard k-epsilon湍流模型，自由液面跟踪方法采用VOF模型，建立三维溃坝波数值计算模型。并针对经典的180°弯曲河道模型实验，进行了不同网格密度和湍流模式的数值计算，验证了数值模型的可靠性，并从中选取出适合弯曲河道溃坝波运动的湍流模式和网格密度。

在此基础上，进行了120°和90°弯曲河道溃坝波的数值计算，结果表明，河道对溃坝波传播的影响程度随弯曲程度的减小而增大。在通过弯道时，溃坝波在凹岸处的水位高于凸岸。

关键词：溃坝波；标准模型；弯曲河道；流体体积

Abstract

In the vast territory of our country, there are many rivers in the distribution. Abundant water resources make the traffic convenient, but if there is a levee outburst accident, it will also bring huge losses to the lives and property of the people along the coast. So, how to predict the impact range of dam-break wave accurately has important practical significance.

Based on fluent software, this paper uses Standard k-epsilon turbulence model, and the free liquid surface tracking method adopts VOF model to establish a numerical calculation model of three-dimensional dam-break wave. According to the classical 180°curved channel model test, the numerical calculation of different mesh density and turbulence model is carried out, the reliability of the numerical models is verified.

On this basis, the numerical calculation of dam-break wave of 120° and 90° curved channel is carried out, and the results show that the influence degree of river course on the propagation of dam-breaking wave increases with the decrease of bending degree. At the time of passing through the bend, the water level at the concave bank of the dam-break is higher than that of the convex bank.

Kew Wards: dam-break wave; Standard k-epsilon model; curved river course; VOF

目 录

第1章 绪论 1

1.1研究的背景及意义 1

1.1.1 研究的背景 1

1.1.2 研究的意义 1

1.2 国内外研究现状 1

1.3 本文的主要研究内容 2

第2章 数值计算方法 4

2.1 基本方程 4

2.2 湍流模型 5

2.2.1 Standard k-epsilon 模型 5

2.2.2 RNG k-epsilon 模型 5

2.2.3 Realizable k-epsilon 模型 5

2.2.4 Standard k-omega 模型 5

2.3 多相流模型 5

2.4 有限体积法 6

2.5 本章小结 6

第3章 数值模型验证 7

3.1 模型的建立 7

3.1.1 模型尺寸 7

3.1.2 初始条件设定 7

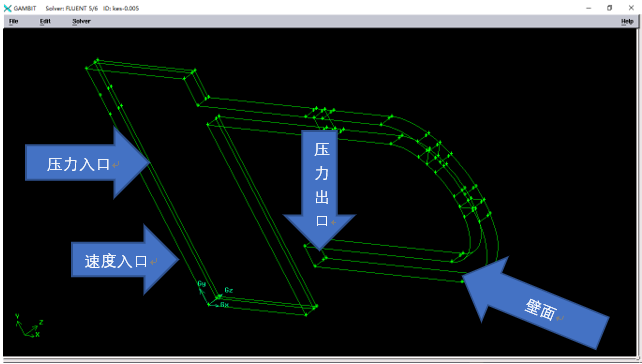
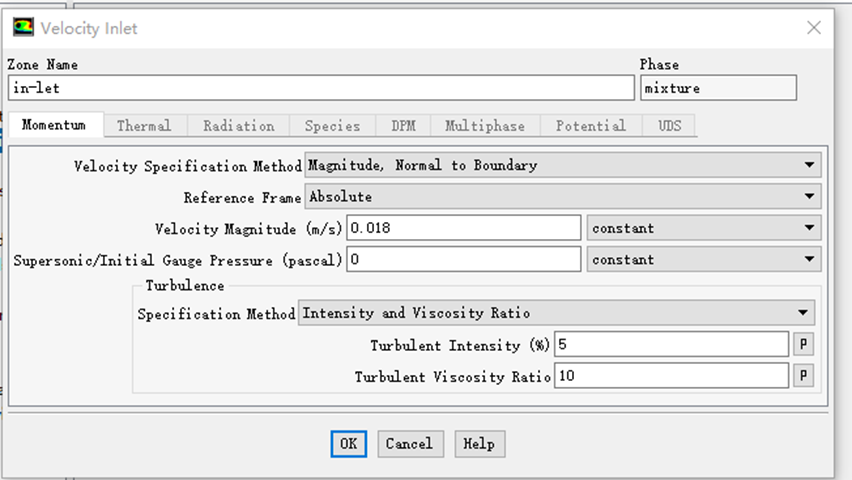
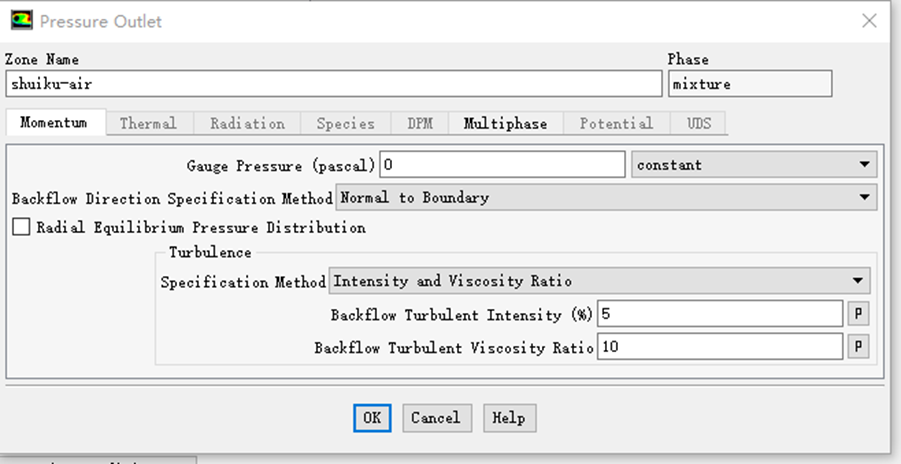
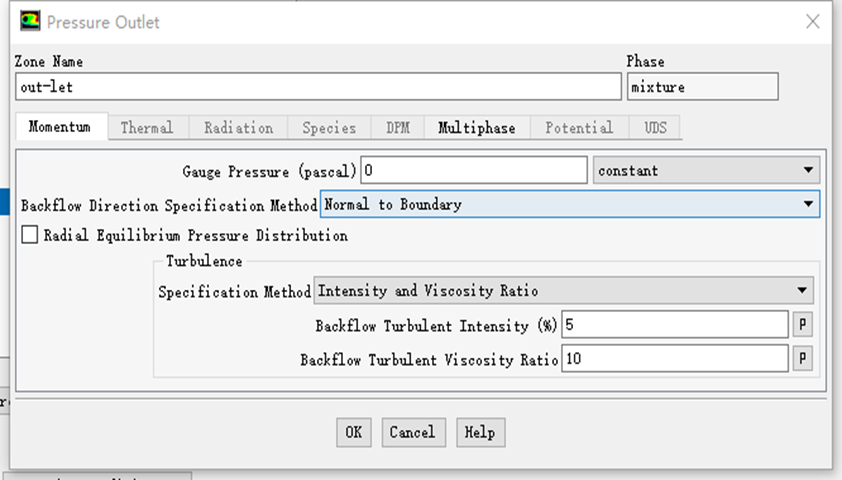
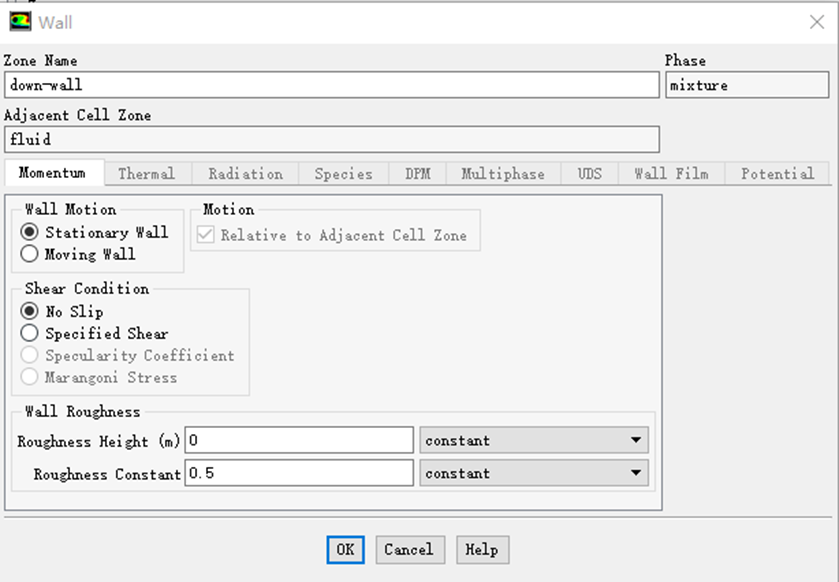
3.1.3 边界条件 8

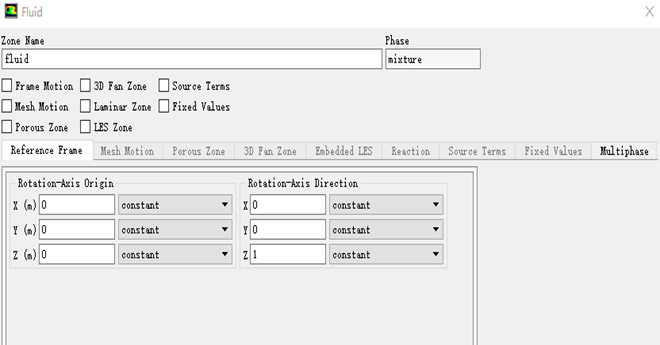
3.1.4 流体区域设置 10

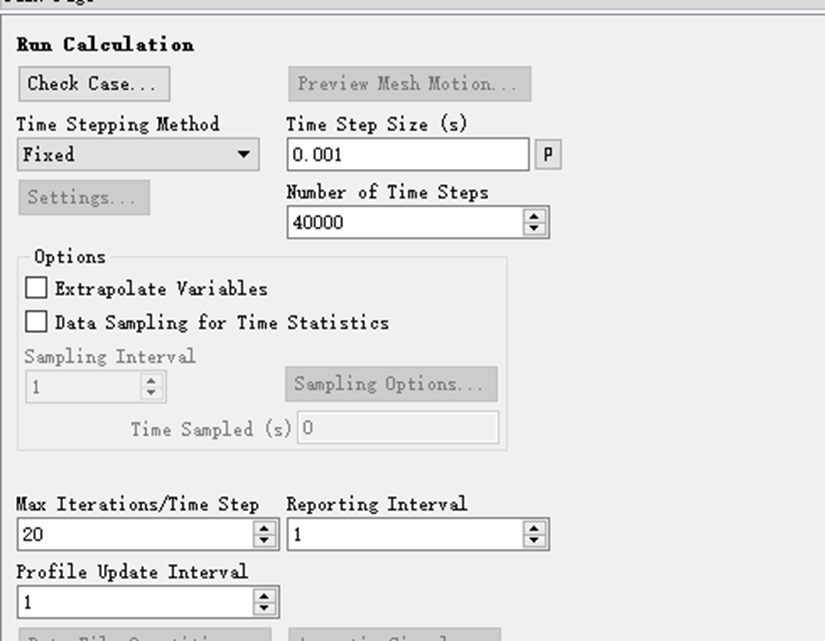
3.1.5 计算步长 11

3.2 计算结果对比分析 11

3.2.1 不同网格计算值与实测值的对比 12

3.2.2 不同的湍流模型计算值与实测值之间的对比 15

3.3 湍流模型和网格划分方式的确定 17

3.4 本章小结 18

第4章 不同弯曲度下的溃坝水流特性 19

4.1 模型的建立 19

4.1.1 模型尺寸 19

4.1.2 边界条件 20

4.1.3 初始条件 21

4.1.4 网格划分 21

4.2 结果分析 21

4.2.1溃坝波水位变化特点 21

4.2.2 溃坝波流速分布特点 23

4.2.3 弯曲河道溃坝波横断面水位分布特点 26

4.3 溃坝波波前传播特点 32

4.4 弯道水流特点的理论分析 34

4.5 数值模拟结果与理论的对比分析 35

4.6 本章小结 36

第5章 总结 37

参考文献 38

致 谢 40

第1章 绪论

1.1研究的背景及意义

1.1.1 研究的背景

在我国辽阔的疆域上，河流纵横，全国1km²以上的湖泊2800多个，流域面积在100km²以上的河流有50000多条，1000km²以上的河流1580条，河流总长约43万公里。对于平原冲积河流而言，通常根据其河床演变形态和演变特征分为弯曲河道、分汊河道、顺直河道、游荡河道四种类型。其中弯曲型河流在世界上分布很广，同时也是最基本的河型。为了满足防洪、发电、引水等多方面的需求，河道上修建了许多拦水堤坝。由于我国大部分中小型堤坝修建时间较长，且受历史条件制约，设计标准偏低；此外超标准洪水、暴雨、地震和滑坡等不可抗力因素的影响，有可能发生溃坝的危险。溃坝波的运动速度以及破坏力远远大于一般的洪水，因此，溃坝一旦发生，将会对下游的人民财产安1全、农业、工业等带来巨大损失。现将近年内，国内外发生的较为严重的溃坝事件列举如下：

（1）2008年9月8日，在山西襄汾发生了尾矿库溃坝事件^[1],事故造成了下游500米左右的矿区办公楼、部分民宅和集贸市场损毁垮塌，近300人遇难。

（2）2010年9月21日，由于台风“凡亚比”影响^[2]，位于广东省信宜市钱排镇的石花地水电站大坝发生溃坝，造成22人死亡以及大量财产损失。

（3）2018年7月，老挝南部Xe-PianXe-Namnoy水电站^[3]大坝发生坍塌，事故造成了35人死亡，99人失踪。

综上所述，一旦发生溃坝事件，将会给下游带来巨大的人员伤亡和经济损失。

1.1.2 研究的意义

挡水建筑物发生破坏以后，水体失去阻挡，在河道中以一个远大于一般洪水的流速向前推进，对水工建筑物及两岸城镇的破坏程度是非常大的。考虑到实际的溃坝波的水流强度大且容易突然发生，破坏性强，造成水利学者很难获取实际的观测数据。并且由于水流运动的复杂性，现在并没用一种通用的计算方法可以对溃坝运动进行精确计算，数值模拟研究、物理模型实验是目前国内外研究溃坝波运动的主要手段。

综上所述，在进行溃坝波水里特性的研究中，数值模拟分析方法是一种非常普遍且成果较为突出的一种研究方法。但是由于问题的复杂性，完全解决溃坝波的精确预报尚有一定的距离。有鉴于此，本文拟基于通用CFD软件—FLUENT，进行弯曲河道溃坝波运动数值计算，为进一步预测溃坝灾害、防灾减灾提供参考。

1.2 国内外研究现状

严培、王鑫等^[4]运用数值模拟的方法，研究在不同弯道曲率与直线段的组合下的水流

流态，寻求减少弯顶冲刷的规律。王嘉松、何友声、倪汉根^[5]利用YVD格式的有限差分算法思想，建立了守恒型浅水方程有限体积的高分变率计算模型，预报了溃坝波的演进过程。李婷^[6]针对石泉大坝溃坝事件，运用溃坝洪水分析以及洪水演进的数值模拟技术，分析了在不同的设计水平年下，溃坝洪水水位、淹没范围等结果。徐娜娜^[7]通过FLUENT软件，建立了二维数值模拟模型，分析不同溃决模式下的溃坝波以及不同河道工况下的溃坝波，为估算唐山堰塞坝发生溃决事故后可能会造成不利影响的洪水影响范围提供了参考依据。白玉川、许栋^[8]从二维的角度建立溃坝水流运动的数学模型，符传君、练继建^[9]以及曾丹、刘成林、陈宇豪^[10]则从三维的角度建立数学模型，为溃坝水流的计算提供了便利。于洋、艾丛芳、金生^[11]对同一曲率半径、水深、渠宽、边界条件下，不同弯曲度的明渠弯道进行三维数值模拟。史常乐、牛兰花、杜林霞^[12]通过MIKE11模型对某山区河流在综合治理过程中产生的溢流堰进行溃坝模拟，分析其发生溃决后的水动力过程，为以后的工程建设提供了数据支持。陈淑婧等^[13]利用BREACH模型、DB模型和IWHR模型，以唐家山堰塞坝1/3溃坝为工程背景进行数值模拟分析，为溃坝计算中的参数选取提供了参考依据。Shaolin Yang、Wanli Yang、Shunquan Qin、Bing Yang^[14]系统地比较研究了下游水深对溃坝波的影响。Liu WJ、Wang B、Chen YL、Wu C、Liu X^[15]通过溃坝实验验证了一维重力波模型的有效性。刘慧^[16]通过物理模型实验研究溃坝波的水动力特性，将实验结果与理论结果对比，归纳分析了理论解的适用性。

一些学者也从其他方面研究溃坝波的运动规律。Z.H.Gu、H.L.Wen等^[17]通过建立三维接口保持水平集方法来模拟大坝决堤问题。将预测数据和实验结果进行对比，成功地模拟了坝体断裂流。José S、Antunes do Carmo等^[18]建立了考虑高色散效果的溃坝波模型，对近岸的溃坝波进行了预报，并通过与实验数据的比较，证明了该模型的有效性。Luca Cozzolino等人^[19]提出了一种新的有限体积方案，进行了多孔浅层水方程中溃坝问题的求解，与精确的溃坝结果进行了比较，证明了其优点。Omid Seyedashraf、Mohammad Mehrabi、Ali Akbar Akhtari^[20]提出了一种基于计算智能系统的经典一维溃坝流问题建模方法，并对其进行了测试。提出的一种新的基于最佳拟合模型的单片方程，可作为现有分段解析方程的有效替代方法。

综上所述，在溃坝波的研究中，数值模拟分析方法是一种非常普遍且成果较为突出的一种研究方法，成为了研究溃坝洪水特性的一种趋势。

1.3 本文的主要研究内容

本文基于FLUENT软件平台，进行了不同弯曲度河道溃坝波运动的三维数值计算，获得溃坝波波前传播特性、水位、流速变化等特点，并以此分析不同弯曲度河道对溃坝波运动特性的影响。主要研究内容如下：

1.针对180°弯曲河道溃坝波模型实验，建立数值计算域，采用Gambit软件进行网格划分。为了探究网格密度对计算结果的影响，一共进行了三种不同密度的网格划分。

2.采用ANSYS下的计算流体力学模块FLUENT，自由表面采用VOF方法进行跟踪，建立三维溃坝波的数值模型，针对上述的三种网格，选取不同的湍流模式，如Standard k-epsilon，Standard k-omega或Realizable k-epsilon模型进行计算。将计算值与实测值进行比较，选取出适合弯曲河道溃坝波运动的湍流模式和网格密度。

3.在此基础上进行120°、90°不同弯曲度的河道溃坝波的数值模拟计算，得到了不同弯曲度三维溃坝波的流场数值解。

4.根据数值计算结果，分析了溃坝波的传播、河道弯曲度对溃坝波的影响、流速分布和水位变化等特点。

第2章 数值计算方法

弯曲河道溃坝波的运动是复杂的、具有自由表面的紊动问题的运动。本文采用数值模拟的方法进行弯曲河道溃坝波的研究。数值模拟的关键在于紊动的模拟和自由表面的追踪。本章将介绍三维溃坝波数值计算方法，为下一章数值模型的验证奠定基础。

2.1 基本方程

连续性方程

（2.1）

式中：u为x方向的流速分量,v为y方向的流速分量,w 为z方向上的流速分量。

，，分别为x，y，z 3个方向上可流动的面积分数。

动量方程

（2.2）

（2.3）

（2.4）

式中：为可流动的体积分数， 为水的密度，p为作用在流体微元上的压强， ，,分别为x，y，z 3个方向上的重力加速度, ，，分别为x，y，z 3个方向上的黏滞力加速度。

湍流动能k方程

（2.5）

耗散率 方程

（2.6）

式中 ： 为紊动的运动黏滞系数

（2.7）

是紊动能的产生项

（2.8）

（2.9）

=0.09，=1.44，=1.92，=1.0，=1.3，=4.377，=0.012。

2.2 湍流模型

2.2.1 Standard k-epsilon 模型

Standard（标准） k-epsilon 模型是在求解湍流问题中最常用的一种模型，该模型本身计算稳定性好，求解精度高而且适用范围广。标准模型通过求解湍流动能和耗散率方程得到的计算湍流黏度，适用于完全湍流的流场，流体间的分子黏性力可以忽略。

标准模型适用于多数湍流问题，但在有旋流等非均匀湍流 问题的计算中稳定性较差。

2.2.2 RNG k-epsilon 模型

RNG k-epsilon 模型Standard模型基础上进行了一些改进，在e方程中增加了条件，使得计算流场时精度有所提高。针对标准模型旋流较弱的问题改善了旋转效应，提高了旋转流动问题的计算精度；Standard模型适合高雷诺数的完全湍流问题，而RNG模型对于低雷诺数的问题也同样适用。

2.2.3 Realizable k-epsilon 模型

Realizable（可实现） k-epsilon 模型是Standard模型和RNG模型的补充，该模型采用了新的湍流黏度公式，耗散率也添加了新的传输方式方程。Realizable模型最大的特点是能够满足雷诺应力约束条件，因此能够保证与现实湍流相同的雷诺应力，在模拟射流扩散速度，旋转速度，流动分离和二次流动等问题有较好的效果。

Realizable模型的缺点在于，在计算旋转和静止区的流场计算问题时不能提供自然的湍流黏度，并且会产生非物理湍流黏性。

2.2.4 Standard k-omega 模型

k-omega模型也是双方程模型。Standard（标准） k-omega 模型考虑了低雷诺数的情况、可压缩性和剪切流扩散等问题，在射流计算，尾流计算，剪切流计算等方面有着广泛的应用。

2.3 多相流模型

FLUENT提供了VOF模型，Mixture模型，Eulerian模型和Wet Steam模型共四种模型。在本文中采用的是VOF模型。

Hirt和Nichols在1981年提出了VOF法。其基本原理是在网格上定义一个函数F，然后根据不同时刻流体在网格单元中占的体积函数F构造以及追踪自由表面。当F=1时，则说明该单元全部被流体充满；当F=0，则说明该单元全部被气体占据，单元为空；当0lt;Flt;1时，则说明该单元部分被流体占据。

F的输运方程为

（2.10）

2.4 有限体积法

有限体积法也称作控制体积法。中心思想是将计算区域划分成一系列的互不重复的控制体积，并保证每个网格点周围都有一个控制体积。然后通过待解微分方程来对每个控制体积进行积分运算，以此可以得到一组离散方程。

离散方程的物理意义，可以理解为因变量在有限大小的控制体积中的守恒原理，类似于微分方程表示因变量在无限小的控制体积都得到满足，那么在整个区域中就得到满足。

就离散方法而言，有限体积法可以看作介于有限单元法和有限差分法的中间物。有限差分法的技术成熟、精度可选并易于编程，但在处理不规则区域时，其局限性较强；有限单元法则适用于处理复杂的区域，精度可选，但内存和计算量过大，而且并行计算不如有限差分法直观；有限体积法则适用于流体计算，对于不规则的网格也可运用，适用于并行。

有鉴于此，本文采用有限体积法来进行计算。

2.5 本章小结

本章节主要讲述了三个方面的内容：首先主要介绍了溃坝水流运动的控制方程，是进行数值模拟计算的理论依据。其次介绍了本文采取的数值模拟计算的模型。最后介绍了有限体积法，解释了什么是有限体积法，使用有限体积法计算有哪些优缺点。

第3章 数值模型验证

弯曲河道中的溃坝波运动是复杂的水流现象，本章将针对典型180°弯曲河道模型实验，采用上一章的数值计算方法，建立数值模型。并探讨不同的湍流模型和网格密度对计算结果的影响。

3.1 模型的建立

本文通过FLUENT进行了溃坝水流在半圆形弯道传播的数值模拟研究，并且与Sky Miller和M. Hanif Chaudhry的半圆形弯道溃坝实验数据进行对比，以此验证所建模型的合理性。

3.1.1 模型尺寸

以上是毕业论文大纲或资料介绍，该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取，微信号：bysjorg。

相关图片展示：