英语原文共 16 页，剩余内容已隐藏，支付完成后下载完整资料

稳定非牛顿流体圆柱绕流：一个数值研究

概述：研究稳定不可压缩非牛顿流体圆柱绕流的电力法指数在0.2到0.4的范围，堵塞比率为0.037，0.082和0.164三种和雷洛数为Re=1,20,40，使用流函数/涡度方程。控制方程是通过使用一个二阶准确的有限差分方法来确定阻力系数，尾流场，分离角和流动形式并探讨权力指数，堵塞比和雷诺数对其的影响。这里报告的结果提供了基本明确的在工程流体参数对阻塞比和幂律指数依赖的窗台和进一步表明，在流线和异涡模式，这导致从增加的影响阻塞率与幂律指数降低的结果相似。

1、引言

圆柱绕流问题代表了一个流体力学中的经典问题而且在学术作品中受到了相当的关注。因此，最近几年牛顿流体的圆柱绕流问题吸引了来自于大量实验、翻译、数值计算方面等领域的兴趣。对这些调查的文章表明，充足的知识体系（特别是对总工程的预测参数，如拖动，唤醒特性等）大多数情况下在牛顿流体通过一个很长的圆柱体作用非常，虽然仍然有一些有关流体中详细结构的尚待解决的问题。显而易见的是在工业实践中遇到的很多材料显示的是非牛顿行为，典型的例子包括聚合物熔体和他们的解决方案，多层多混合物（悬浮液，乳液，泡沫）和肥皂液的解决方案等。在综合设计的支撑结构和桥墩暴露于非牛顿泥浆，电线和薄的钢瓶使用在非牛顿流量测量探头和传感器中，在一个非牛顿的大颗粒输送的浆管中的管线设计中，对水下物体如球体和圆柱的水动力的了解是必要的。其他在聚合物加工操作中也有类似的例子，比如埋在表面形成焊接线的运用。除开的这些可能的运用，这儿有一个内在理论旨在阐明非牛顿流体的作用结构和高度理想化的形似球缸的阻力。尽管具有如此重要性和频繁发生的非牛顿流体，少有人对非牛顿流体的圆柱绕流进行相关的研究。即使对于最简单的，也可能是最常见的非牛顿行为类型，即剪切变稀和剪切增稠行为。这种类型流体行为经常采用简单双恒功率法模型建模。这项工作着手调查的稳定幂律流体二维圆柱绕流。然而，这对于概括总结之前文献中对当下问题的方程不足之处的结果是有意义的。

从理论的角度来看，只有非常有限的研究体现在学术报告作品中。坦纳发现在零雷诺兹数的限制下，没有斯托克斯悖论为剪切变稀流体而剪切增稠与它仍是相关的。这显然是因为在远离气缸的时候剪切率急剧增加。对于剪切变稀流体，这意味着在逐步增加粘滞力而粘滞力减少剪切增稠流体，随后其他人也得出了类似的推论。坦纳获得渐变流体的幂律流体圆柱绕流的切力变稀流体的近似分析结果。他还补充了在n=0.4—0.9范围内的结果与数值预测。这些对应关系被发现是合理的，随后，这些结果一直延伸到更小的幂律指数低达n=0.2。然而，所有这些结果只涉及到零雷诺数和剪切变稀流体行为。达莱西奥和Pascal数值研究了幂律稳定流绕圆柱在雷诺Re=520并用第一阶精度差分方法固定阻塞比beta;=0.037，其中beta;定义为气缸直径与从外部边界到气缸表面距离的比值。他们研究了关键雷诺数，尾流长度，分离角和阻力系数的幂律指数的相互关系。他们的报告中说，作为雷诺兹数的价值是逐步增加有一个递减的收敛程度限制的范围幂律指数的可能的数值解。因此，例如当Re=20，他们能够得到的只是弱非牛顿流体完全收敛的结果，此外，它们的表达式计算的阻力由于疏忽遗漏的一个因素似乎是错误的，幸运的是，它对其尾流特性、流体模态的其他结果的没有什么影响。然而，它对于确定上述参数对气缸表面到外部边界的距离的依赖性也是很重要的（堵塞的影响），这是因为在近似有限程度的流动中这个距离有所增加，或者说等价于减少壁面稳定的非牛顿流体流过圆柱的影响。

虽然对牛顿流体和非牛顿流体的粘弹性，堵塞对流动参数/流水线模式堵塞效果已经以及数值模拟和实验在渐变流区域的结果被很好的记录下来，但对非牛顿流体的黏性幂律的相关研究仍然缺乏。当下研究的目标是扩展达莱西奥的研究工作而帕斯卡使用更精确的的有限二阶有限差分方法，更加精准的计算网格和更大的幂律指数范围来研究堵塞对阻力系数、尾流长度、分离角和广域状态的流体模态的影响（流线和等值涡度等值线）。

2、基本原理

从理论的角度来看，稳定不可压缩流体幂律流体过去用很长圆柱的连续性和动量方程描述。迎面而来的稳定不可压缩流体是在正常的圆柱体轴线的方向。由于圆柱轴线沿着z轴方向的无限延伸，所以流动可看做二维的，流动与z轴无关切z方向的速度等于0。连续性方程和圆柱坐标运动方程组的r和h的参数可以用极坐标方程（ε，ф）表示且ε=ln（r/a），并给出极坐标方程：

（1）

Epsilon;分量

（2.1）

和ф分量

（2.2）

无尺度流函数psi;，涡度omega;和压强p都跟它们的无因次量纲的关系分别为和，其中U是流体流速，a是圆柱半径，rho;是流体密度。额外的应力张量无量纲的成分T_ij与其量纲之间的关系为，而雷诺数Re被定义为：

（3）

其中K表示幂律的一致性指数，n表示幂律指数。对于剪切变稀流体而言nlt;1，而ngt;1则为剪切增稠行为。对于一个幂律流体的本构方程写为：

（4）

其中ŋ是无量纲粘度，而ε_ij是速度-变形张量里面的无量纲因子。

幂律无量纲粘度方程为：

（5）

其中I₂是给定的变形张量率的二次不变无量纲单位定为：

（6）

和

（7）

在其缩放形式的涡度为：

（8）

消除压力方程。通过交叉分化的方法，介绍了涡X与一些 重排得到：

其中

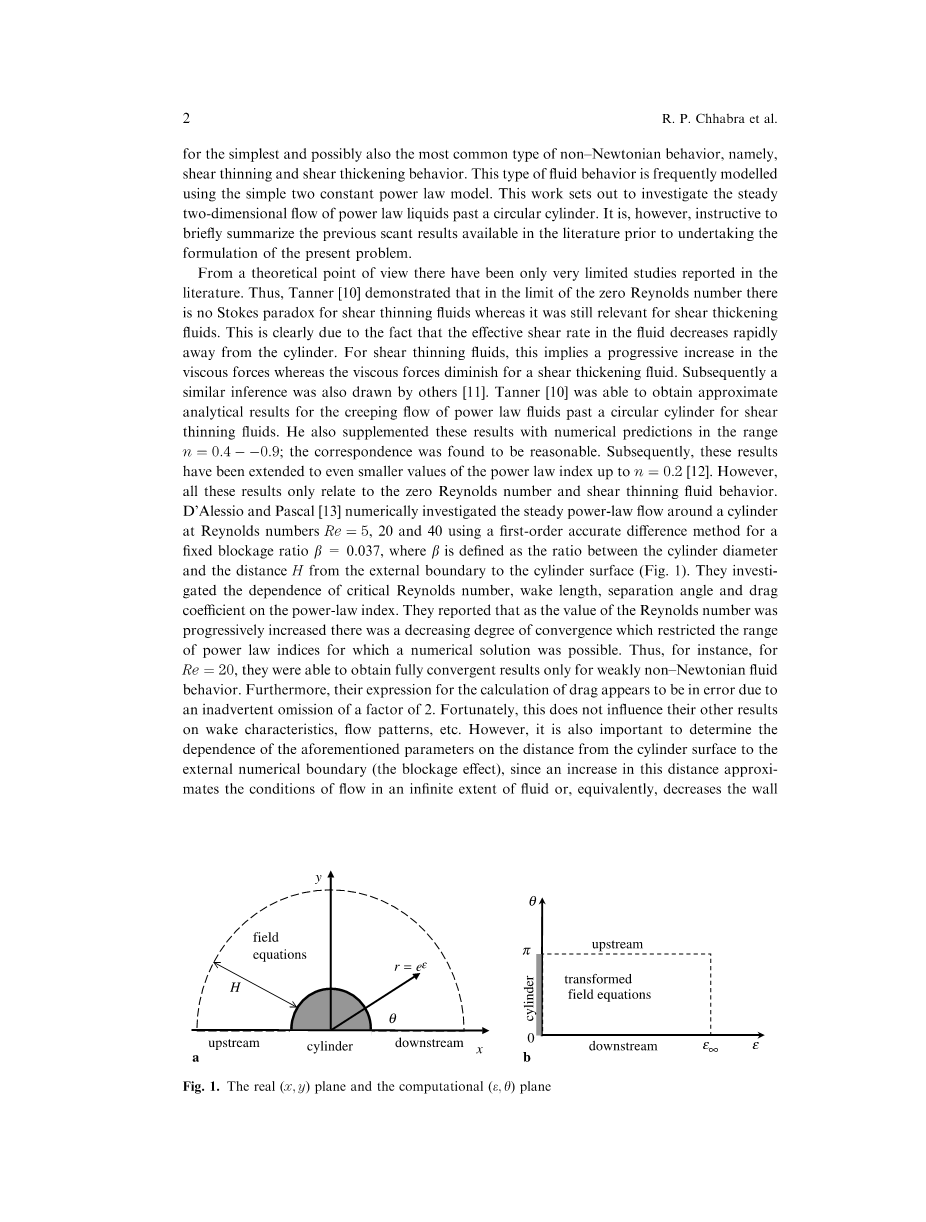
由于问题的二维性质，而即将到来的来流是x方向的。我们只需要考虑ygt;=0和x² y²gt;=1这个区域，因此对应的区域被定义为εgt;=0和0lt;theta;lt;pi;(图表1).

边界条件如下分布：

在墩柱表面，通常无滑移条件的应用，即

联立方程8得到

沿着x方向

由于流函数和涡度方程的椭圆性质，它是必要的外部边界建立边界条件，即距气缸较远处的边界条件。今井给出了流函数的渐近公式并且一般将涡度作为牛顿幂律流体的外边界条件，在极坐标下，外部边界条件中w和x被插入到今井方程的粘度方程。给出了两者的外部边界条件（无论是在缩放和无量纲形式）。

稳定非牛顿流体流经墩柱，

其中Cd是阻力系数。

而函数（Q）是标准误差函数。适当的补充一下在此处n=1。公式16公式17减少到非牛顿的情况，而且不同于那些达莱西奥和Pascal的0.5和1.4的数值因素。它们对应的错误出现在方程中，因为它们没有减少到预期限制行为Nfrac14;1牛顿。流函数和涡度的指数缩放是适当的，因为流体功能是大于远离缸的流体，和除了在该地区的唤醒，涡度指数变小。对于用于外部边界条件，本研究中，缩放程序保持零和1之间的值，从而抑制了数值不稳定性。

而一旦w和psi;的值知道，那么阻力系数的值可以由下式给出：

其中psi;是实空间中的无量纲涡，I₂是无量纲在真实空间中的形变张量的二次不变的速度通过真实空间中无量纲流函数的插入，把psi;=e^-z带入方程6中。最后，它是同时适当的添加在这里，因子2在最右边的项的分母，方程（18）是从13对应的方程。

3、数值求解方法

计算域的数值解显示在图表1b.中，由于共有（N 1）times;（M 1）个网格，在E的间距和h-directions分别为E1 = N。控制流函数和涡度方程（8）和（9）是改写为fi有限差分方程的二阶精度的中心差分。二阶迎风差分技术[ 21 ]求解方程（9）与片面性—分近似x的fiRST衍生物。数字，这种技术产生了三—对角矩阵，对角占优，因此，无条件稳定。这个二阶迎风差分技术是优先于本研究中应用中心差分近似，由于初步试验表明，后者的方法导致数值不稳定，这个与其他作者的观察相一致。为控制方程的稳态解，即流函数（方程（8）），涡度（方程（9））和幂律粘度（方程（5）），用高斯赛德尔获得松弛迭代法[ 23 ]。为了获得所有变量的一致逼近，迭代扫描是通过网格点和阻力系数的更新值通过方程的数值积分确定（18）在气缸表面采用辛普森规则。

图2a中阻力系数（Cd）作为一个幂律指数函数（n）和阻塞率（B）重新frac14;1其中临界功率法指数n_e－0.8。在图2b中，阻力系数（Cd）作为一个幂律指数函数（n）而且堵塞比（B）在雷诺数重新调整为frac14;20为临界幂律指数数控制在0.42plusmn;0.08；阻力系数（Cd）作为一个幂律指数函数（n）和阻塞率（B）在雷诺数重新调整为frac14;40，临界幂律指数数控制在0.40 plusmn;0.05。

对于图3a，分离角作为一个幂律指数函数（n）和阻塞率（B）雷诺数被重新调整为frac14;20；对于图3b，分离角作为一个幂律指数函数（n）和阻塞率（B）雷诺数被重新调整为frac14;40。

为了获得收敛，申请在0.5个松弛因子和1的涡量变量是必要的。重复的迭代过程，直到阻力系数发生变化，每一次迭代小于10^-10。W和x的初始化计算得到每个网格点使用下面的公式，这主要是在理想流体的前提下。

稳定的非牛顿流体的圆柱绕流

在图4a中尾迹的长度（L）为一个幂律指数函数（n）和阻塞率（B）而雷诺数被重新确定为frac14;20；在图b中，尾迹的长度（L）为一个幂律指数函数（n）和阻塞率（B）而雷诺数被重新确定为frac14;40。

和

由此获得的初步值，然后用于确定牛顿流体中w和x的值，这反过来又被用来作为初始猜测的非牛顿流体。这个程序保证了数值解的加速收敛性。在本研究中所用的所有的计算网格的径向步长大小为0.02而且H角步长为1.8°雷诺数被重新调整为frac14;20，40。除了在雷诺数frac14;1时，在这些步骤的大小翻了一番。我们进行了不同的步骤大小的额外的测试表明，上述步长是适当的因为他们发现提供足够的数值解析。

每个雷诺兹数和幂律指数的数值解，得到使用三个不同阻塞率的矩形计算网格。当雷诺数等于frac14; 20, 40 时对应的网格数为200 · 100, 160 · 100 和125 · 100。但是对于Re frac14; 1 时，网格数为100 times;50, 80 times; 50 和 62 times; 50。在所有的情况下，外边界位于E的frac14;4，3.2和2.5倍，对应的渐近边界条件的距离为54.6，24.5和12.2个气缸半径。相应的阻塞率B是近似值，约为0.037、0.082和0.164。

上述数值方法测试了牛顿流体在雷诺数的范围在1到100以内时的情况，结果和其他作者有很好的一致性。因为在雷诺兹数大于40的时候流动变得不稳定，在模拟稳定流动时，在此范围之外没有任何实际意义。因此，只有在雷诺数大于40时才会被用到。而且，在Bfrac14;为0:164时没有n低于0.6，在b frac14;为0.037时n不会低于0.2或者 Re frac14; 1时Bfrac14;为0.082或者0.3以下时对应Bfrac14;为0.3.在本研究中使用的数值不稳定，这是发现发生较低的值n和更高的值b，而这可能是由于在气缸表面上的涡度的增加幅度降低。这样的数值不稳定产生发散或振荡的结果。

流量参数，如阻力系数Cd，分离角theta;和尾迹的长度L，对于N 1.4和Refrac14;1值计为20和40，而且和下面的行为是相应的。在我们的工作中，对非牛顿流体流动模式的结果，雷诺兹数字高达40。在Re为frac14;40时从筒分离并形成一对站立旋涡，但还不稳定（图8）。不幸的是此处并无实验证明。

利用幂律流体中墩柱绕流验证数值计算结果。本研究，如下所述。

1. 结果和讨论

结果表明，每个Refrac14;为1，20和40时，阻力系数的变化与幂律指数是非线性的，与Tanner 一致。Ferreira 和 Chhabra 还有 Whitney 和Rodin，对于 Re frac14; 1，阻力系数达到Nfrac14;0:4（图2A），与Tanner 与幂律流体墩柱绕流的结果一致。这样的一个高峰，然而，Whitney和 Rodin是做不到的。在高雷诺数下（ (Re frac14; 20, 40），没有这样的峰，观察和有一个整体的增长阻力系数与幂律指数（图2b、c）。它也被发现有一个临界幂指数nfrac14;数控的阻力系数几乎成为独立的阻塞率，这一值在雷诺数从1到40时记录从n_c=0.8到n_c=0.40 0.05（图2）.此外，对于控制的数值ngt;n_c，阻塞比的增加总是导致的阻力系数的增加（图2）。目前的结果表明一个非线性的幂律指数的阻力系数的变化不同于那些达莱西奥和Pascal，由于他们漏遗了2的一个因素的对阻力系数的表达。然而，我们的研究结果之间的详细比较那些达莱西奥和Pascal 的结果表明，这种疏忽没有显著地影响他们关于变化的流线与幂律指数在固定堵塞比为（Bfrac14;0:037）的发现。此外，结果表明，无论是分离的角度和唤醒长度是强烈依赖于幂律指数为20和40，这些参数达到他们的最低值约n =0.4到0.6（图。3和4）.对于幂律指数值大于0

剩余内容已隐藏，支付完成后下载完整资料

资料编号：[148537]，资料为PDF文档或Word文档，PDF文档可免费转换为Word