基于GA-SVM的数控机床热误差建模研究毕业论文
2020-02-17 22:00:35
摘 要
本文主要是对基于SVM的数控机床热误差建模的研究,主要从关键温度测点选择,SVR热误差回归建模,GA遗传算法寻优三个方面展开研究。运用遗传算法对SVM的惩罚函数、核函数参数和不敏感损失函数对多工况条件下的优化选择,建立机床主轴的热误差预测模型。
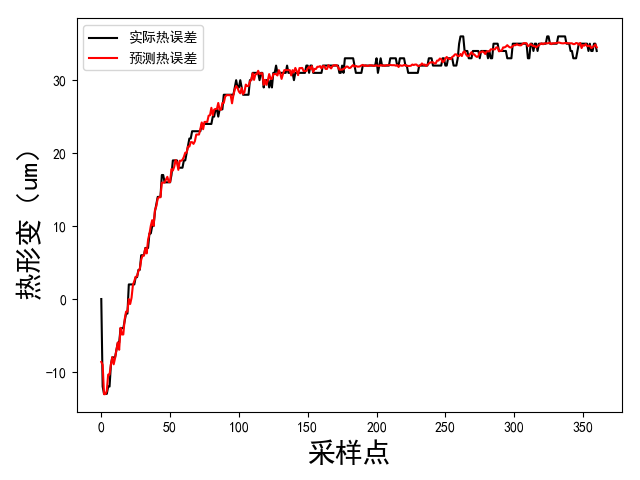
论文主要研究了武重ZK5540数控机床主轴旋转产生的温度和机床主轴结构变形之间的关系。首先是获取得到数控机床主轴温度数据和热误差形变数据(Z轴),然后筛选主轴温度数据获取关键温度点,通过SVR来预测拟合温度和误差之间的关系,其中SVR中三个参数受GA遗传算法控制,遗传算法负责寻找最优三个参数来得到SVR模型。
研究结果表明:通过遗传算法可以自动寻找SVM的相似最优三个参数,所得到的SVR模型具有良好的预测误差效果。
本文的特色:所有的实验数据均来自武重机床实际测得数据,并且编程实现GA-SVM的热误差建模方法,真正的来解决实际问题。
关键词:数控机床;关键温度测点;支持向量机;遗传算法
Abstract
This paper is mainly about the research of thermal error modeling of CNC machine tools based on SVM. It mainly studies three aspects: key temperature measurement point selection, SVR thermal error regression modeling and GA genetic algorithm optimization. The genetic algorithm is used to optimize the SVM's penalty function, kernel function parameters and insensitive loss function under multi-case conditions, and the thermal error prediction model of the machine tool spindle is established.
The paper mainly studies the relationship between the temperature generated by the rotation of the spindle of Wuzhong ZK5540 CNC machine tool and the structural deformation of the machine tool spindle. The first is to obtain the CNC machine tool spindle temperature data and thermal error deformation data (Z-axis), then filter the spindle temperature data to obtain the critical temperature point, and predict the relationship between the fitting temperature and the error through SVR, where the three parameters in the SVR are GA genetic algorithm control, genetic algorithm is responsible for finding the optimal three parameters to get the SVR model.
The research results show that the genetic algorithm can automatically find the similar optimal three parameters of SVM, and the obtained SVR model has good prediction error effect.
The characteristics of this paper: all the experimental data are from the actual measured data of Wuzhong machine tool, and the GA-SVM thermal error modeling method is programmed to solve the actual problem.
Key Words:CNC machine tool;Critical temperature measurement point;Support Vector Machines;Genetic algorithm
目 录
第1章 绪论 1
1.1 课题研究的背景、目的及意义 1
1.2 国内外研究现状 1
1.3课题研究内容和预期目标 3
第2章 基于遗传算法的支持向量机建模 4
2.1 关键温度测点选择 4
2.1.1 灰度关联分析法 4
2.1.2 模糊聚类分析法 5
2.2 支持向量机 6
2.2.1 分类超平面 7
2.2.2 对偶问题求解目标函数 9
2.2.3 Kernel核函数 10
2.2.4 SMO最小序列优化算法 13
2.2.5 从SVM模型到-SVR模型 14
2.3 遗传算法 14
2.3.1 遗传算法原理 14
2.3.2 基于GA-SVM的热误差建模 15
第3章 数控机床热误差模型实验验证 17
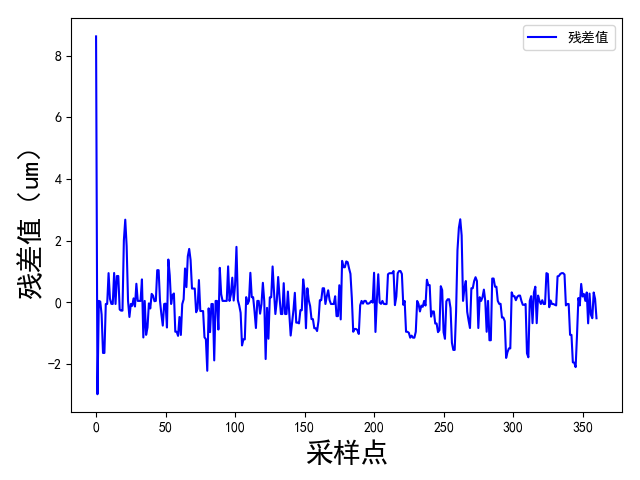
3.1 温度测点优化分析 17
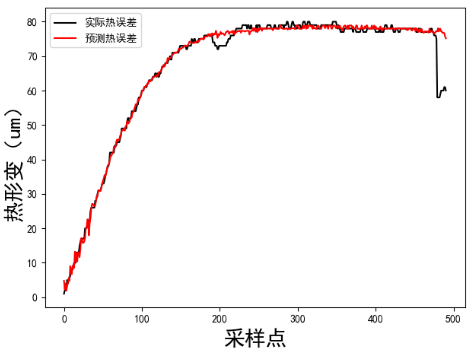
3.2 两种工况热误差建模 19
3.2.1 恒速空转工况 19
3.2.2 变速空转工况 22
3.3 工况模型泛化预测 24
第4章 总结与展望 26
4.1 总结 26
4.2 展望 27
参考文献 28
致 谢 30
第1章 绪论
1.1 课题研究的背景、目的及意义
装备制造业越来越成为国之重器,尤其是在在当今高速发展的社会中,对国家的综合国力有着重大的影响。而现代制造业一般都由数控机床来完成制作,既能提高效率,又能节省人工成本,但一些装备对精度的要求越来越高,给数控机床带来了很大的压力。从影响数控机床精度的因素来看,机床温度所导致的精度偏差占了很大的影响。数控机床热误差是指的当机床温度升高时造成了制作精度的误差。根据实验研究显示,导致数控机床产生误差最大的是热误差,总共占到了总误差的40%-70%左右,因此,减少热误差就成为了数控机床提高精度的主要目的,降低机床热误差的方法主要包含有误差防止方法和误差补偿方法这两种方法[1],对于误差补偿法来说,可以从软件方面来补偿热误差,这就是本篇论文需要完成的事情。
本次课题研究的目的在于通过提出软件方面的方法来有效的解决机床的热误差问题,使机床精度能够得到一定的提高,软补偿方法是通过建立数控机床热误差模型,通过此模型对引起误差的温度数据进行预测位移误差,在已经存在的表现误差条件下,通过采集实验数据来建立数学模型,将得到的预测误差值人为的通过硬件对表现误差进行补偿,以此来相互抵消。通过这次课题的研究,将为解决数控机床的热误差问题提供一种合适的解决方案,进一步提高数控机床的精度。
1.2 国内外研究现状
数控机床热误差补偿技术的研究最早起源于瑞士,上个世纪30年代左右,瑞士学者通过对坐标镗床进行测量分析后,发现数控机床在运行所中产生的热形变会对定位加工的精度产生非常重要的影响[2]。从那时起,世界上各国学者对数控机床的热误差进行研究,到了上世纪50年代,国内也开始了热误差补偿技术的研究,经过若干年的发展,国内高校开始对数控机床补偿技术展开了广泛的研究[3],并相继提出了许多热误差建模的方法,例如:BP神经网络,灰色关联分析,动态神经网络,支持向量机,叶贝斯网络等建模方法。
在中国,由上海交通大学杨建国教授领导的研究小组对数控机床误差补偿进行了一系列研究。其中,为了便于收集机床温度和热变形,杨建国团队等人开发了一种机床热误差检测系统,可以方便快捷地收集机床的温度和主轴热变形。在温度临界点优化筛选技术中,他们利用灰色关联度理论优化和消除温度点,提出了温度点布置的优化策略[4]。
浙江大学林伟青,傅建中等人提出了基于LS-SVM与遗传算法的数控机床热误差辨识温度传感器优化策略,在数控机床热误差识别过程中,引入遗传算法对温度传感器进行滤波,大大降低了温度变量的数量。使用LS-SVM方法的回归建模产生了高建模精度。充分利用遗传算法和LS-SVM的结合,数控机床的热误差模型更加实用有,大大减少了数控机床热误差补偿的实施成本[5]。
河北工程大学的魏效玲,张宝刚等人提出了基于GA-BP网络的数控机床热误差建模研究,研究表明,GA-BP热误差模型具有处理时间短,预测误差精度高,收敛速度快等特点[6]。
浙江大学现代制造工程研究所开发了具有16通道数据采集能力的温度和热误差检测系统。该系统使用DS18B20数字温度传感器来检测温度,通过涡流位移传感器检测热误差并具有高精度,CCD激光位移传感器收集温度和热误差数据,并使用ARM开发板将其传输到计算机[7]。
清华大学机械系的王海同,王立平等人针对理论和实际的热误差建模这两种研究方法做了进一步的分析,讨论之间的优缺点,并对数控机床未来的发展做出了展望[8]。
Bing Ren, Xiaohong Ren等人提出了机床热误差建模与补偿研究,利用PSO-BP神经网络建立了测量温度参数与热误差参数之间的补偿模型。最后开发了用于实现误差补偿的热补偿控制器[9]。
Baomin Wang等人提出了电机主轴热误差的动态建模,提出了一种新的热误差模型(ARX模型),该模型利用了主轴热弹性系统具有复杂动力学特性的概念,利用热误差敏感技术,给出了建立鲁棒性热误差模型所必需的温度关键点的选取原则[10]。
Jian Lee,Dong-Hyeon Kim等人做了关于机床高速主轴特性的实验研究,基于有限元法和热分析方法,对40000转高速机床主轴的热特性进行了研究和试验。对主轴系统进行了有限元分析,得到了不同转速对主轴系统温度分布、温升和热变形的影响[11]。
而国外对数控热误差补偿技术的研究要早与国内。在1993年,美国密西根大学的Chen J.S等人将几何误差和热误差加以结合分析考虑,建立了综合误差模型,通过结合时间与和三维空间域,在之前的21项几何误差的基础上,重新定义了包含热形变的11项热误差在内的新的32项总机床误差[12],并且针对不同类型的热误差,他们分别建立了热误差补偿模型。
Ali M. Abdulshahed等人提出了ANFIS预测模型在热误差中的应用对数控机床的补偿,集中采用自适应神经模糊推理系统(ANFIS)来设计两个热预测模型,ANFIS将数据空间划分为矩形子空间(ANFIS网格模型)和ANFIS使用模糊c -means聚类方法(ANFIS-FCM模型)[13]。
1.3课题研究内容和预期目标
本次论文主要是以武重ZK5540机床为实验对象,本文主要概括了数控机床的国内外研究现状,然后通过对机床采集的数据进行灰度关联处理,建立支持向量机回归模型,整篇论文可分为如下四章。
第一章:主要介绍这次课题研究的背景、目的和意义,进一步分析了国内外对数控机床热误差补偿技术的研究,阐明课题研究内容以及要达到的目标
第二章:主要分析灰度关联算法原理及实现,支持向量机的数学原理及推导,遗传算法原理及实现。
第三章:主要是对数控机床热误差模型进行研究与实验,通过对所采集的实验数据进过模型预测,将模型推广适用于多工况条件,验证GA-SVM模型能更好的适应于数控机床的热误差建模
第四章:主要是对本次论文的总结与展望,分析论文完成的主要内容,提出还需改善进步的部分。
第2章 基于遗传算法的支持向量机建模
本部分内容主要分为以下三个部分:关键温度测点选择,也就是从多个温度点中提取几个与热误差关联度大的温度点,剔除那些影响较小的温度点,这样可以来降低工程的时间和空间复杂度;支持向量机,建立温度数据与热误差的基本模型,可以通过此模型来预测误差;遗传算法,对支持向量机中三个参数进行适应度分析寻优,找到最适合模型的三个参数。
2.1 关键温度测点选择
要进行关键温度点的选择,目前来说有两种常用的方法,灰度关联分析法和模糊聚类分析法,前者根据温度数据与热误差的关联度大小来选择关键温度点,后者是根据温度数据间的相关性来将温度数据进行聚类分组。
2.1.1 灰度关联分析法
灰度关联分析法的具体步骤如下:
1)首先要确定实验数据,包括原始的温度数据和误差数据,温度数据xi ={xi(k) | i=1,2…,n; k=1,2,…m}[14],误差数据x0={ x0 | k = 1,2,…,m},其中n表示温度数据的种类,m表示每一组数据的个数
2)将所有的实验数据进行无量纲的归一化处理,这里的归一化是将每一列数据进行归一化[14],即用该列每个数据与该列最小数据的差值除以该列最大值与最小值的差值,具体公式如(2.1)
(2-1)
式(2.1)中,是归一化后的数据,是实验数据(温度数据和误差数据)
3)计算温度数据与热误差数据之间的灰色关联度。首先计算温度数据xi对误差数据x0在第k点上的关联系数
(2.2)
其中为分辨系数,一般取0.5,为两级最小差,为两级最大差,一般来说,的值越大,分辨率越大,值越小,分辨率越小[14]。
4)计算各列温度数据与热误差数据的关联度,通过将3)中的每一列关联系数取平均值即可求得每一列温度数据与误差数据的关联度[14]
(2.3)
最后将所有的关联度进行从大到小进行排序,选择前几个关联度大的温度点作为实验的关键温度测点。灰度关联分析法算法流程图如下:

图2.1 灰色关联算法流程图
2.1.2 模糊聚类分析法
模糊聚类方法是采用模糊数学的方法来对数据进行聚类分析,模糊聚类分析方法的具体步骤如下:
1)根据相关系数法可以建立每个数据的相关系数,所有的相关系数组成模糊相似矩阵,设为n个温度变量数据的集合,其中为X中第i个温度数据的m个实验数据值,则相关系数矩阵的每个值可以由如下公式求得:
其中 (2.4)
2)当我们得到模糊相似矩阵后,还不足以能够满足分类要求。能够进行分类的矩阵必须要满足自反性、对称性、传递性这三个条件[14],模糊相似矩阵不一定具有传递性这一特性,所以我们需要将其转化为模糊等价矩阵,这里将采用传递闭包法来进行处理[15],具体公式如下:
(2.5)
当满足时,令
(2.6)
此时,就是我们所需要的模糊等价矩阵
3)当我们得到模糊等价矩阵后,矩阵里的每一个值的范围都是0-1,所以我们可以选取一个阈值,当时,令其值为1,小于时则为0,这样可以将R中所有的值归零或归一,然后再比较列值是否对应相同,当R中某两列值相同时,可以将这两列归为同一类,依次类推就可以分出所有的温度变量的类型。模糊聚类算法流程图如下:

图2.2 模糊聚类算法流程图
2.2 支持向量机
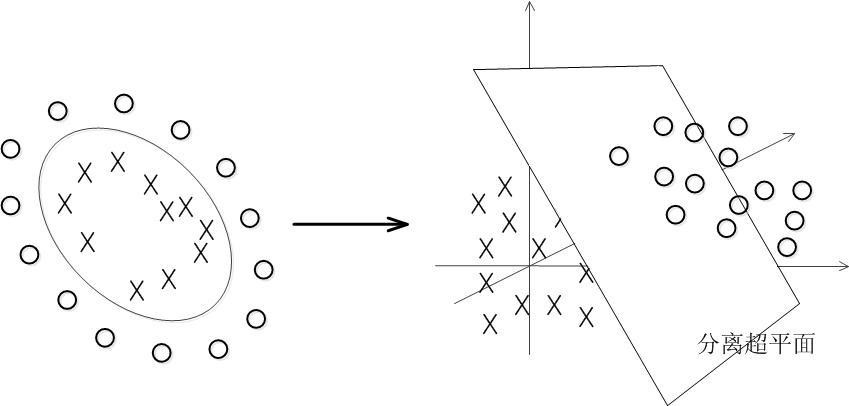
支持向量机其实是一种分类器,它可以将一堆数据进行分类,其原理是通过寻找分割
超平面来实现的。作为监督学习中最有效的分类方法,将会从以下几个方面来展开:提出分类超平面的定义,引入函数间隔与几何间隔,然后给出目标函数以及约束条件,这样就知道要优化求解哪些参数;用拉格朗日乘数法建立目标函数和约束条件的函数,更新目标函数形式,将其转化为对偶问题来求解,求得的w和b依赖于一组参数值;对于非线性问题,需要引入核函数来将目标函数从低维度映射到高维度,同时在低纬度完成运算,另外对一些特殊点引入惩罚因子C来进行处理;对于值的求解,可以采用SMO序列最小优化算法;在SVM的的分类前提下,引入了不敏感损失函数过渡到-SVR模型来对温度数据进行热误差的预测,这才是模型的实际意义所在。
2.2.1 分类超平面
如图2.1所示,图中是一个二维的数据组成的平面,数据点分别用圆圈和叉来表示,每个点的值代表的是输入数据x是二维的,当规定直线上方对应点的输出y是1,下方是-1,则可以将这两类数据分开,此时数据线性可分,而分开数据的直线可以看做是二维的“分类超平面”。
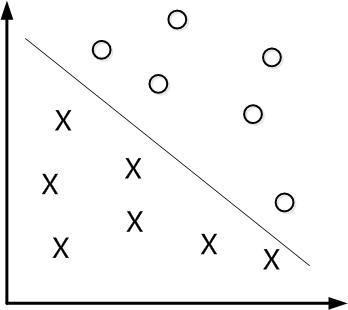
图2.3 线性分类示例
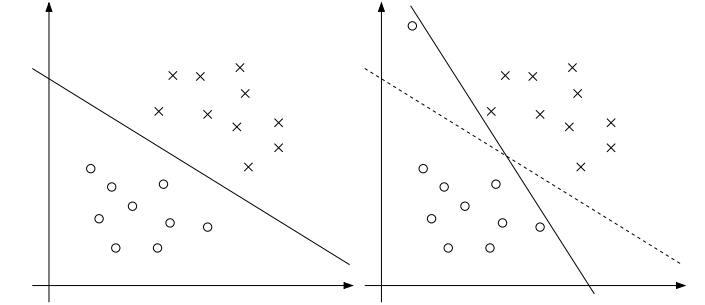
下图2.4中,这个分类超平面的表达式是,当大于0时对应的是y=1的数据点,当小于0时对应的是y=-1的数据点,当等于0时,对应的就是分类超平面。其中x的维度是一维,红色标记的是支持向量机的点,就是支撑起这个超平面。
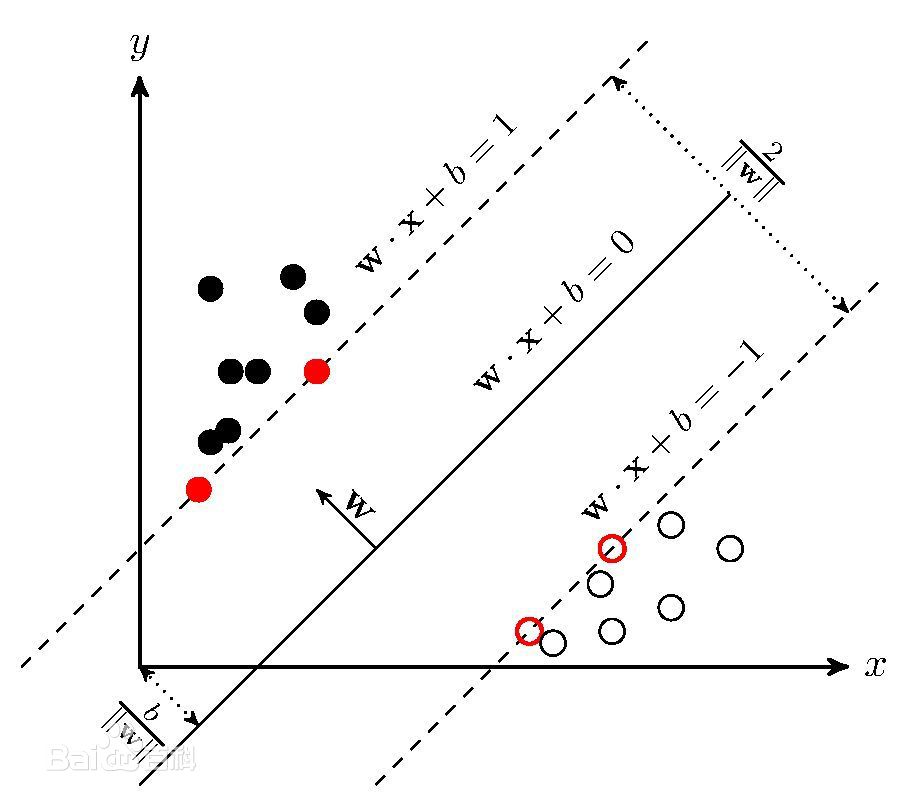
图2.4 分类超平面
有了分类超平面的概念之后,可以通过定义分类函数间隔和几何间隔来推到得出目标函数。
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: