基于粒子群算法TSP研究与应用毕业论文
2020-02-17 21:46:41
摘 要
旅行商问题是一个多项式复杂程度的非确定性问题,其在路径规划、管道布置等方面有着重要的应用,因此任何能够解决此问题的方法都值得研究。而粒子群算法作为一种进化算法,以随机解为起始点,通过多次迭代来寻找一个最优解,与遗传算法一样均通过适应度的值来评判解的优劣性,但粒子群算法规则相较遗传算法要更为简便,因此将粒子群算法应用于旅行商问题具有一定的优势和研究意义。
本文针对旅行商问题,采用了一种改进的粒子群算法,通过将交叉和变异引入粒子群算法,来降低粒子群算法陷入局部最优的几率,从而提高全局搜索能力。
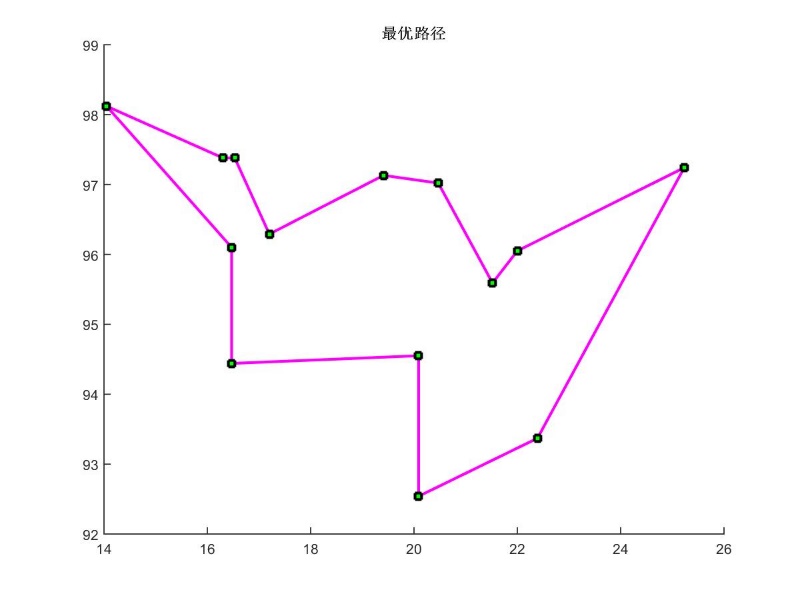
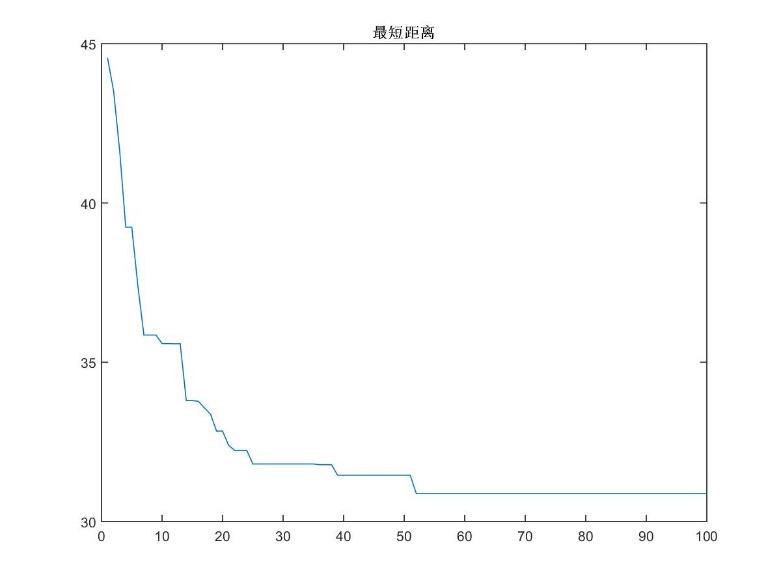
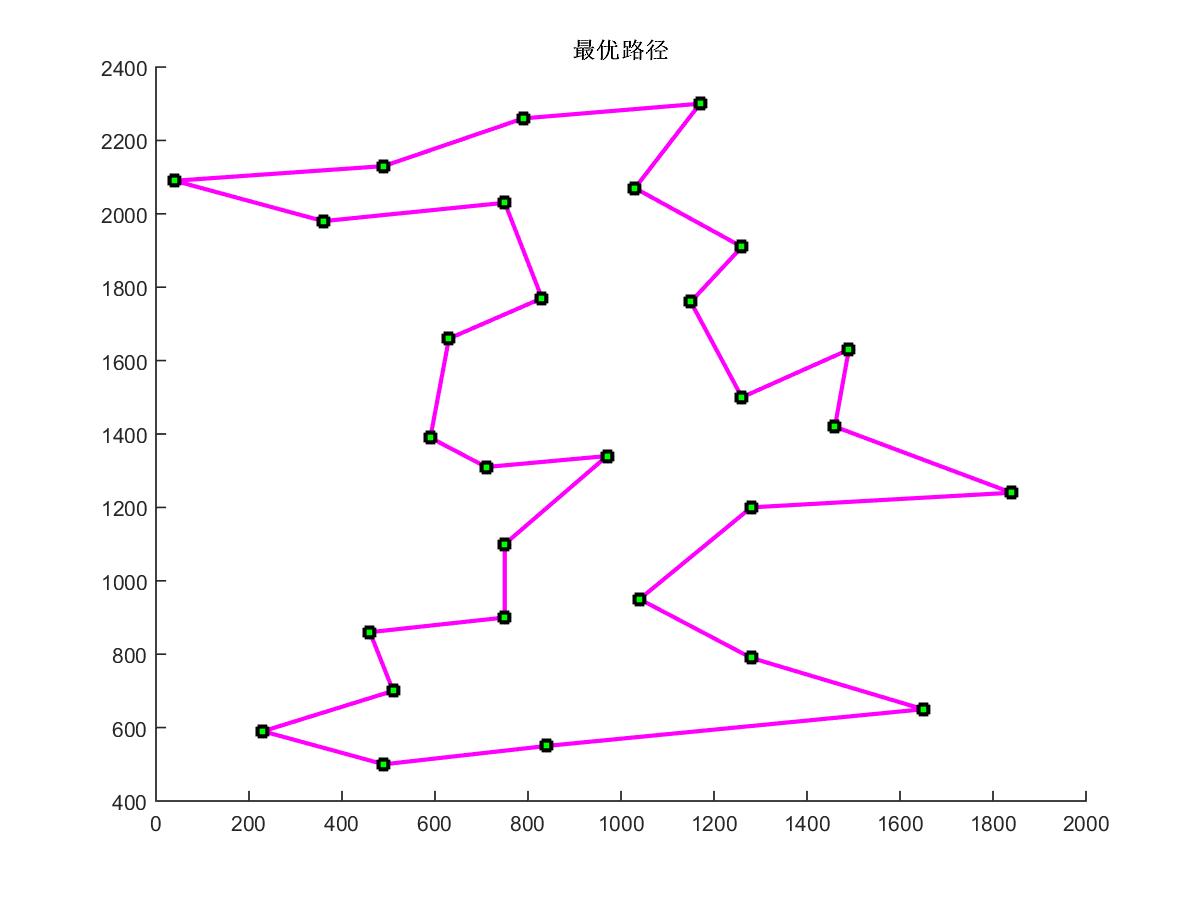
本文在Matlab软件中进行了仿真实验,采取Berma14、Bayg29、Eil51标准数据集进行实验,结果表明引入交叉和变异的混合粒子群算法能够在误差控制在较小范围内的条件下解决旅行商问题。
关键词:粒子群算法、旅行商问题、优化、交叉和变异
Abstract
Travelling Salesman Problem is a nondeterministic problem of polynomial complexity, which has important applications in path planning and pipeline layout, so any method that can solve this problem is worth studying. Particle swarm optimization (PSO) , as an evolutionary algorithm, takes the random solution as the starting point, and iterates many times to find an optimal solution However, particle swarm optimization (PSO) rules are simpler than genetic algorithms, so the application of PSO to Travelling Salesman Problem has certain advantages and research significance.
In this paper, an improved particle swarm optimization (PSO) Algorithm is proposed to reduce the probability of particle swarm optimization (PSO) falling into local optimum by introducing crossover and mutation into PSO, thus improving the global search ability.
This paper carries out simulation experiment in Matlab software, and uses Berma14, Bayg29, Eil51 Standard Data set to carry on experiment, the results show that the hybrid pso with crossover and mutation can solve the Travelling Salesman Problem problem under the condition of error control in a small range.
Keywords: Particle swarm optimization, Travelling Salesman Problem, optimization, crossover and mutation
目录
第1章 绪论 1
1.1 研究背景及意义 1
1.2 国内外研究现状 1
1.2.1 粒子群算法研究现状 1
1.2.2粒子群算法在TSP的应用现状 2
1.3 本文组织结构 3
第2章 TSP问题研究 4
2.1 TSP问题分析 4
2.2 TSP问题建模 5
2.3 TSP问题算法研究 5
2.4 本章小结 6
第3章 粒子群算法研究 7
3.1 基本粒子群算法研究 7
3.1.1 算法原理 7
3.1.2 算法流程 9
3.1.3 算法优缺点 10
3.2 改进粒子群算法求解TSP 11
3.3 混合粒子群算法研究 12
3.3.1 遗传算法 12
3.3.2 混合粒子群算法 14
3.4 本章小节 15
第4章 混合粒子群算法求解TSP问题研究 16
4.1 流程设计 16
4.2 计算适应度及更新粒子 17
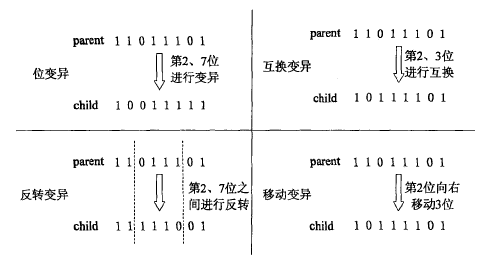
4.3 交叉和变异操作 17
4.4本章小节 19
第5章 实验仿真及结果分析 20
5.1 实验环境 20
5.2 算法测试 20
5.3 本章小节 24
第6章 总结与展望 25
6.1 本文工作总结 25
6.2 今后工作展望 25
参考文献 26
致谢 28
第1章 绪论
本章主要介绍了本论文所钻研内容的背景和近况,并提出本文选择的解决问题的方式,最后对本文的章节布置进行了简略描述。
1.1 研究背景及意义
旅行商问题(TSP)是一个古老的优化问题,传统的解决方法包括弗洛伊德算法、迪杰斯特拉算法等,但是随着问题规模的增大,这些传统算法耗费的时间和存储空间急剧增加。对于城市数目较多的大规模旅行商问题,常规递归搜索算法难于在规定的时间内获得满足要求的解。但由于旅行商问题具备普遍的实际应用价值,例如巡检线路安排、电商物流配送路线选择、共享汽车车站选址决策、区域地下管道铺设线路设计以及生产制造中切割路径的划分等问题都能转化为旅行商问题模型,而在取得全局最优解的难度巨大时,研究人员们转而开始寻找计算出误差较小的次优解的方法。近年来,研究人员们在许多自然现象中受到不少启发,提出了多种基于自然界的生物群体运动规律的搜索方法,并且在旅行商问题领域获得了成功应用。目前求解旅行商问题的启发式群智能算法包括蜂群算法、蚁群算法、人工鱼群优化算法以及粒子群优化算法等。
粒子群算法又叫做鸟群觅食算法,它属于一种进化算法,在算法初期随机生成一个解,通过既定的优化策略进行多次迭代来寻找一个最优解,直到达到最大迭代次数。粒子群算法评判解的优劣性是通过适应度的大小来体现的,对于组合优化问题,适应度越小,则算法所求解出的最终解越优秀。粒子群算法的算法规则相较其它群智能算法要更为简便,因此粒子群算法目前被广泛运用于实际中。
由于旅行商问题在实际生活中的应用程度不容忽视,任何能够以高效率准确求解该问题的方法,都值得我们关注并加以思考。因此,本文所探讨的基于粒子群算法来解决旅行商问题这一课题具备很高研究价值。
1.2 国内外研究现状
1.2.1 粒子群算法研究现状
1995年,心理学研究者Kennedy和计算智能研究者Eberhart共同在IEEE国际神经网络学术会议发表了文章《粒子群优化》,这是粒子群算法第一次以正式的身份登上学术舞台,该文章提到粒子群优化源于两种主要的方法,且它与人工生命的联系尤其明显,特别是与鸟类群集、鱼类学校教育和群集理论的联系[1]。同时,它也与进化计算有关,并且与遗传算法和进化编程都有联系。
1999年,研究人员M. Clerc发表的文章《蜂群与蜂后:自适应粒子群优化算法》提出了一个非常简单的粒子群优化迭代算法,只有一个方程和一个社会/置信参数。文章定义了一个“无希望”收敛准则和一个“再次希望”方法,使得群体根据目标函数的一些梯度估计和之前的更新行为,不时地重新初始化它的位置,这意味着它具有一种非常基本的记忆能力[2]。该方法通过考虑群体重心,即“蜂后”而得到改进,其结果足够好,因此在更复杂的问题上尝试该方法是值得的。
2002年,来自普度大学工程与技术院的学者Parsopoulos K E.发表了文章《多目标问题的集体智能优化》,提出将拉伸技术用于粒子群算法的优化问题的求解,这种技术可以克服粒子群算法易陷于局部最优值的缺点[3]。
2006年,王翠茹、冯海迅等学者在粒子群优化算法中引入了速度变化机制和粒子自我探索机制,使得粒子不仅能够调整自己的飞行速度,还拥有在一定程度上吸取其它个体经验的能力,这种新的学习方式与鸟群的进化规律更加相像,因此粒子更容易搜寻到旅行商问题的全局最优解[4]。同时他们还提出了调整因子和调整序的概念来重新定义粒子群算法。
1.2.2粒子群算法在TSP的应用现状
高尚、韩斌、吴小俊、杨静宇等学者在文章《求解旅行商问题的混合粒子群优化算法》中将遗传算法和粒子群算法的思想进行结合,提出了一种混合粒子群算法,把粒子不断趋向于最优解的过程定义为遗传算法里交叉因子对染色体的作用,将变异因子当作惯性项,用以求解一些还未很好解决的组合优化问题[5]。
钟一文、杨建刚、宁正元等学者在文章《求解TSP问题的离散粒子群优化算法》中对粒子的运算规则给出了新的定义,即添加了学习因子和排斥因子[6]。
曹平、陈盼、刘世华等学者又提出了将模拟退火算法引入到粒子群算法中的新想法,用以解决优化中的旅行商问题[7]。
傅刚在《PSO-TSP问题综述》中谈到,在非连续域中能否以高效率解决旅行商问题的关键在于平衡粒子个体经验和群体经验对粒子迭代过程中运动的影响[8]。
旁巍、王康平、周春光等学者通过引入模糊矩阵的概念,重新规定了迭代过程中粒子的速度更新公式和位置更新公式,并用模糊矩阵来表示每个粒子的运动信息,这种算法的提出也是求解旅行商问题的一种新方法[9]。
郭文忠、陈国龙等学者在分析惯性权值在粒子群算法中所起的作用的基础上,开创了一种惯性权值的模糊自适应调整策略,改进后的粒子群算法在更新同一代种群时采用不同的惯性权值[10]。实验将这种算法用于旅行商问题的求解,结果表明改进后的算法性能比基本粒子群算法高,算法运行所耗费的时间也更短。
易云飞、陈国鸿等学者提出了基于k-means的改进粒子群算法求解旅行商问题,对粒子的位置和速度更新公式进行了改写,同时初始种群的诞生用到了贪心算法的思想[11]。基于k-means的改进粒子群算法为避免过快陷入局部最优,在最初将粒子群划分为两个独立群体,分别搜寻各自群体的最优个体,再令个体最优间进行交叉的操作,使得整体而言算法搜寻到全局最优解的速度更快,提高了粒子群算法求解旅行商问题的效率。
王文峰、刘光远、温万惠等学者提出求解旅行商问题的自逃逸混合离散粒子群算法,这种算法受到自然界中聚集在同一区域的某个物种数量太多时个体自发寻找新的生活地点的现象启发,阐述了一种自逃逸思想:从候选路径段集合中吸收新路径段,令陷入局部区域的粒子发生变异,使其能够跳出局部区域[12]。这种新算法提高了粒子群算法的全局搜索能力,在很大程度上克服了算法过早得出不正确结果的缺陷。实验结果表明,自逃逸混合粒子群算法相比于混合蚁群算法更容易迅速完成算法收敛, 尤其在较大规模的实例上更具优势。
1.3 本文组织结构
本文主要完成旅行商问题的粒子群算法求解,采用Matlab软件完成代码书写以及仿真。通过更改实验参数,可以解决不同规模的旅行商问题。
第一章为绪论。介绍了论文所选课题的研究背景及意义、此课题的国内外研究发展现状以及本文对此所选择的解决方法,并对本论文的研究内容以及论文组织结构进行了说明。
第二章为基本粒子群算法。对基本粒子群算法做了简要介绍,囊括了其算法原理、算法流程和算法优缺点。
第三章为旅行商问题。介绍了旅行商问题的含义、其数学建模方法和目前已知的两种解决旅行商问题的方法大类。
第四章为基于混合粒子群算法的旅行商问题。本算法以基本粒子群算法为基础,为了克服粒子群算法容易陷入局部最优的缺点,同时提高粒子群算法解决旅行商问题的精确度,结合遗传算法中的交叉和变异操作,得出一种混合粒子群算法用以解决旅行商问题,本章对论文中这种混合粒子群算法的实现进行了说明。
第五章为仿真实验及结果。介绍了仿真实验所选取的标准数据集和不同实验中选取的不同参数,并对实验结果进行了扼要的分析。
第六章为总结与展望。对所完成的工作进行总结,并对算法的进一步完善提出改进意见。
第2章 TSP问题研究
本章介绍了旅行商问题的含义,以及如何用数学的方法为其建立模型,最后分析了旅行商问题的精确算法和近似算法。
2.1 TSP问题分析
旅行商问题(TSP ,Traveling Salesman Problem)背后的想法是由奥地利数学家Karl Menger在20世纪30年代中期提出的,他邀请研究团体从数学的角度从日常生活中考虑一个问题:一个旅行推销员必须在若干个城市中的每一个城市访问一次,然后返回家乡,他知道从任何一个城市到另一个城市的旅行距离,那么他应该如何选择路线最为合适?如图2.1所示,该问题实际上是要在一个闭合的加权无向图中,研究出一条总权值最低的汉密尔顿回路,即找出一条通过图中每个顶点一次且仅一次的一条回路,这是一个经典的组合优化问题。
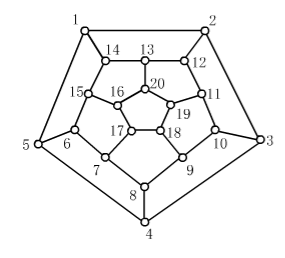
图2.1 汉密尔顿回路
由于该问题的所有解是全部地点的全排列,随着城市数目增加,可选择路径条数急剧变多,因此它是一个NP完全问题。同时旅行商问题还是一个离散问题,这也让问题的解决变得更为复杂。然而,旅行商问题仍然是一个非常有吸引力的问题,因为它作为自然的一个子问题出现在许多涉及日常生活的应用中。因此,研究旅行商问题决不能被认为是一个抽象的、没有实际意义的研究。
在实际生活、工业和科学领域中许多问题都可以简化为以旅行商问题为基础的模型,例如:巡检线路安排、电商物流配送路线选择、共享汽车车站选址决策、区域地下管道铺设线路设计以及生产制造中切割路径的划分等。单一旅行商问题的深入探讨还引发了研究人员对多人旅行商问题解决办法的思考。此外,目前已经有不少学者对经典旅行商问题进行了扩展研究,提出一种时间优化的旅行商问题,其目的并非找出一条总距离最短的回路,而是全程所耗费时间最短的路径[13]。旅行商问题在这一方面的研究应用在游客游览景点的生活情境中将会大大提高旅游效率,从长远看亦可以促进旅游业发展。
2.2 TSP问题建模
对于旅行商问题,我们可以采用数学建模的方式将其用数学公式来表示,以便于理解。
设N为城市数目,令,D为N阶距离矩阵,代表已知的城市i与城市j之间的距离。目的是要找出到访每个城市且每个城市恰好只经过一次的一条汉密尔顿回路,且这条路径的长度要尽可能短。
把回路图记为一个加权图H=(V,E),其中V为顶点集,E为边集。
公式(2.1)引入决策变量:
(2.1)
则目标函数(在粒子群算法中也可以叫做适应度函数)可表示为公式(2.2):
(2.2)
约束条件为:
(2.3)
(2.4)
(2.5)
(2.6)
公式(2.3)和公式(2.4)的含义是对每个城市而言,只有两条与外界相连的道路。公式(2.5)的含义是保证了回路中不会产生任何的子回路,其中S为回路图的部分或全部顶点,是V的非空子集,|S|代表S中所含有的顶点数目。
旅行商问题的定义和数学建模虽然并不复杂,在城市数目只有个位数时使用穷举法可以得到确定的最短路径,但随着问题的复杂性上升,用穷举法列举出所有路径再找出最短路径的工作量是非常大的。所以,城市数目比较多的时候需要找寻新的简便算法。
2.3 TSP问题算法研究
学者们已经对旅行商问题的算法做出了许多研究,大体上包括精确算法和近似算法。
在旅行商问题的研究过程中,有一些特殊的情况已经得出了精确的求解算法,例如Gilmore等人在上世纪60年代提出的工件加工顺序问题、Lawler等人在上世纪70年代提出的二分图情形和Burkard在上世纪80年代提出的一些平面TSP问题的特例等。研究者们己经能够精确求解这些特别案例[14]。
研究人员们首先提出了线性规划算法,线性规划是来自于运筹学的概念,旨在利用数学方法找出某一函数在特定条件下的极大值或极小值。运用于旅行商问题中时,搜寻解的区域划定的范围可看作是该算法中的可行域,寻找最优解的过程即为在约束条件下不断逼近极值。另外,研究者还提出了分支约束算法,这种算法可以理解为线性规划算法的延申,通过改变可行域的边界对粒子的搜寻过程进行调控,从而使粒子逐渐靠近区域中最优解所在的分支,直到最终找出最优解。
动态规划、分支约束这样的精确算法虽然有其优点,但是还存在许多不足之处,比如在城市数目增多的时候所耗费的运算时间长,最重要的是每一种算法都只针对于特定的旅行商问题,这一点在需要批量解决不同规模的问题时是十分不利的。
为此,科学家们又发明了群智能算法,即近似算法。群智能优化算法来源于人们对自然界中不少现象的观察和思考,比如蚂蚁、萤火虫等昆虫群体和鸟群、狼群、鱼群等群居性动物的集体行为,或是水流的融合这种自然景观。拿本论文所研究的粒子群算法来说,其来源是动物群落中的鸟群。一只鸟的个体行为是很简单的,但是当许多鸟聚集起来形成一个群体时却能够进行复杂社会行为,并且不是在某一个个体的指挥下完成的,而是具有自组织性,不同的个体之间存在信息经验交互的方法,通过相互协作,从而适应弱肉强食的外部环境,鸟群才得以生存和进化。
目前已经有不少群智能优化算法得到了研究,除本论文所探讨的粒子群算法外,还包括人工免疫算法、退火算法、禁忌搜索、遗传算法、蚁群算法等等。这些算法的共同点是都是从一个随即构造的解出发,通过与自身特性符合的策略,不断进行迭代,随着子算法的重复运行,也不断获得更优秀的解。群智能算法虽然不能求解出最为精确的旅行商问题的解,但是其计算速度快,所得近似解的误差也能够控制在一定范围以内。
随着对自然界生物和自然现象的抽象、模仿的研究不断深入和发展,群智能优化算法如今已经大范围地运用于数理研究的优化领域和工业规模化生产之中。研究者们将许多这些实际生活中的复杂问题进行简化,抽象成旅行商问题、车辆路径问题和工件生产安排等问题,通过建立数学模型,用近似算法加以解决。
2.4 本章小结
本章首先对TSP问题的内容做了详细的介绍,包括TSP问题的含义分析和TSP问题的数学建模方法;其次介绍了目前已经被学者们研究过的TSP问题精确算法和近似算法。由于精确算法更适合用来解决某些条件特定的TSP问题,而本文的研究目的是解决不同规模的问题,是以本文选择近似算法,即群智能算法来进行研究,由此明确了本文利用粒子群算法求解TSP问题的中心。
第3章 粒子群算法研究
本章由基本粒子群算法的研究引出其在TSP问题上的应用,并提出引入遗传算法中交叉和变异操作的混合粒子群算法。
3.1 基本粒子群算法研究
3.1.1 算法原理
从人类开始从事科学研究以来,研究人员一直对自然界中的许多动物群落的群体行为有着极大的研究兴趣,生物学家Craig Reynold在1987年提出了一个沿用至今的三维立体鸟群群体计算机模型,在他的Boids(Bird-Oid Object)建模中,每一个个体遵循以下规律:
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: