定向DCT及其实现毕业论文
2020-02-17 21:09:00
摘 要
在信号与信息处理之图像压缩这一领域中,离散余弦变换(DCT)是普遍使用的方法。传统的二维DCT方向为沿着水平和竖直方向分别进行两次一维的离散余弦变化。虽然传统二维离散余弦变换功能十分强大,可以解决大部分图像处理问题,然而却没有考虑到图像局部的纹理特性,某种程度上影响了图像压缩技术的发展。为了解决这一缺点,人们开始针对方向离散余弦变换进行了研究,已达到进一步改进编码的压缩效率的目的。
方向离散余弦变换(DDCT)的第一次DCT变换沿当前块的边缘方向进行,第二次的DCT变换仍沿水平方向进行。这种结合图像局部的纹理特性的方向离散余弦变换优于传统DCT的编码特性。
本文首先对传统DCT的原理进行了详细的描述,紧接着从DCT与方向DCT的不同之处入手介绍了DDCT的原理和实现流程,然后以峰值信噪比(Peak Signal to Noise Ratio)作为参考,通过MATLAB语言的实现后,比较在相同情况下DCT和DDCT的效果,最后得出了图像块在边缘含有方向信息的时候,选择方向DCT往往比DCT 的效果更好的实验结论。
关键词:定向离散余弦变换;峰值信噪比; MATLAB
Abstract
Discrete Cosine Transform (DCT) is the main method of image compression in the world and is widely used in the field of signal processing. Although the traditional two-dimensional DCT can be decomposed into two one-dimensional transformations in the horizontal direction and in the vertical direction, and the function is very powerful, most of the image processing problems can be solved, but the texture characteristics of the image are not considered. To a certain extent, it has affected the development of image compression technology. In order to solve this shortcoming, people have begun to study the direction discrete cosine transform, and have achieved the purpose of further improving the compression efficiency of the code.
The first DCT transform of the Direction Discrete Cosine Transform (DDCT) proceeds along the edge direction of the current block, and the second DCT transform still proceeds in the horizontal direction. This direction-discrete cosine transform combining the local texture characteristics of the image is superior to the coding characteristics of the conventional DCT.
In this paper, the principle of traditional DCT is described in detail. Then the principle and implementation flow of DDCT are introduced from the difference between DCT and DCT. Then the Peak Signal to Noise Ratio is used as a reference. After the implementation of MATLAB language, the effects of DCT and DDCT in the same situation are compared. Finally, when the image block contains direction information at the edge, the experimental conclusion that the direction DCT is often better than the DCT is obtained.
Keywords: directional discrete cosine transform; peak signal to noise ratio;MATLAB
目录
第1章 绪论 1
1.1 图像压缩编码及其标准的发展 1
1.2图像压缩的必要性及可行性 1
1.3图像压缩技术 2
1.4 定向DCT的研究意义及其国内外现状 3
第2章 离散余弦变换原理及实现 4
2.1 JPEG的图像压缩基本系统 4
2.2 离散余弦变换 4
2.2.1 一维DCT 5
2.2.2 二维DCT 6
2.2.3 快速离散余弦变换 6
2.3 离散余弦变换的实现 8
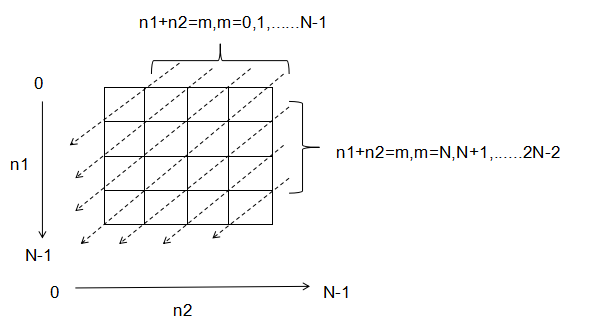
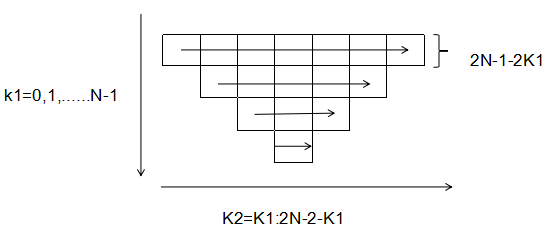
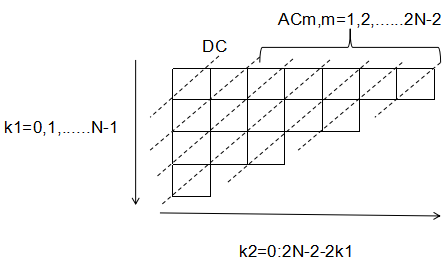
第3章 定向离散余弦变换实现 11
3.1 模2计算过程 12
3.2 模4计算过程 13
第4章 编码实现及实验结果分析 15
4.1 MATLAB介绍 15
4.2 不同量化程度下的DDCT图像变换 15
4.3 基于块变换后系数的比较 16
4.4 DCT和DDCT的PSNR比较 18
4.4.1峰值信噪比的简述 19
4.4.2 相同条件下PSNR比较的实验结果 19
4.4.3 改变量化系数的PSNR 20
4.5 DCT与DDCT变换重建图像的对比 20
4.6实验中出现的问题 21
第5章 总结与展望 23
5.1 工作总结 23
5.2 此课题继续研究的方向 23
参考文献 24
致谢 25
第1章 绪论
1.1 图像压缩编码及其标准的发展
随着计算机技术的发展和问世,图像处理这一科学就随着超大规模集成技术以及计算机结构、性能及算法的不断地发展,并广泛用于科学、生产及生活领域。处于信息在不断高速发展的我们,对科技、多媒体技术等高科技发展也随之迫切需要。当然信息的压缩、传输技术也必不可少。信息时代的重要特性是信息的数字化,因此在对原始图像进行传输和存储之前,必须要对图像信息进行压缩。
在经典的图像压缩编码中,就不得不说到Shannon的信息论。其中,20世纪的五六十年代产生了最基本的预测编码、矢量量化等编码技术影响至今。目前,它们仍然被图像压缩编码的国际标准所普遍采用,随后,人们又对新的编码方法又取得了进一步的发展[1]。
图像压缩的效果判定必然涉及到人的视觉特性。因此一波对人眼视觉特性的研究随着展开,多种编码算法的综合算法和许多结合视觉系统特性HVS都是在改性研究不断深如的过程中提出来的。新一代编码的概念在20世纪90年代以来由Kunt等人提出的,这种编码方法与传统编码基于信号波形变换的方法相比,可能获得更好的图像压缩比,是一种基于对象模型的描述方法。该类新的编码技术冲破了信息论的框架的束缚,实现从“波形”编码到“模型”编码的转变,并且该技术充分利用了人类视觉及图像信源的各种特征,获得了更高的压缩比。若考虑到实用化,它们还受到一定制约,其中最重要的一点就是处理的复杂度,而且对一半图像进行处理时,并没有达到理论上预期效果的编码增益。
上世纪90年代,小波变换编码是另一类受科学家关注的经典编码方法。小波变换提供了多尺度、多分辨率的图像描述方法。随后,分等级树的集分割算法是在小波变换编码的基础上得到的改进,此算法降低了运算的复杂度,也获得了更好的压缩效果。从此小波变换在新的图像编码标准中的奠定了重要地位。
在Internet和无线通信的发展与普及的基础上,还需要考虑抗误码优良性能等。由此确立了标准化工作的进一步发展与完善。目前,国际化标准组织与国际电信联盟已经制定了适用于不同类型数字图像的压缩编码标准。
1.2图像压缩的必要性及可行性
图像压缩这一概念就是为了保证满足目的要求和人眼可忽略的图像质量的基础上,从而达到减少原始图像数据量目的的过程。
图像的数据量非常大是图像压缩编码的必要性。人们对压缩图像数据量的需求越来越迫切,这是为了有效的传输、存储图像信息。随着互联网时代的来临,传输的图像信息种类多样、图像数据量爆炸式增长,通信技术面临的压力也越来越大。若不加大对数据压缩技术发展的力度将无法顺应时代的发展。
据科学家分析指出图像是可以被压缩的,因为构成图像的数据之间有着很高的相关度,所以假设我们可以减少甚至于消除图像数据在符号或者空间等很多方面的相关性,就可以减少比特数对空间的占用最终实现对图像的压缩。在这里,我们分别解释时间冗余、空间冗余、符号编码冗余,时间冗余在于前后帧具有关联;空间冗余则是由相邻像素的关联性引起的。后来逐渐发现,如果我们分别用断码和长码来表示概率高和概率低的符号,这样就可以使得符号编码的冗余得以消除,即可变长编码技术。其实我们的眼睛优势一些图像的变换并不能明显感知,这是一种视觉上的冗余,也可以利用这一点来消除不必要的数据进而起到压缩的作用。
1.3图像压缩技术
下面我们讨论图像压缩编码技术的分类,把不同的物理量作为参考标准就会有不同的分类标准。将压缩过程有无信息损失作为判别标准,可以将图像压缩编码技术分为无损编码和有损编码;将压缩原理作为判别标准,可以将图像压缩编码技术分为三种:预测编码、变换编码和统计编码。使用无损压缩是解压后的还原图像与原始图像基本相同,信息的损失可忽略不计。若想获得较高图像质量的话就使用无损编码;使用有损编码对图像进行有损压缩会丢失掉图像的部分信息,存在了一定的失真,在允许一定失真的条件下,该方法能够达到比较好的压缩比。
编码技术多种多样,但图像变换编码的基本原理基本一致:就是为了改变能量的分布,从而将图像的空间域在变换域中描述。
据信息论学科描述,正交变换对信源熵、信息量、能量等物理量不进行改变,且能对能量这一物理量进行重新集中于分配,是变换后的能量大多集中在直流和低频分量上。以上的正交变换的优势都为图像压缩提供了可能。
在图像变换中正交变换有很多种,常见的有傅里叶变换、离散余弦变化等。在正交变换中离散傅里叶变换算得上是鼻祖了。在均方差误差最小意义下K-L变换是相对最优变换,去相关性是该变换的最大优点,因此在处理图像在变换域的数据的旋转和压缩时候要用到;当然二维K-L变换也是存在不可忽视的缺点,那就是不可分离性,这造成了复杂度很高的问题,同时在变换中必须要计算图像数据关于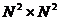 协方差矩阵的特征值和特征向量这两个物理量,庞大的计算量使这种变化难以得到应用。综上所述,最优且应用最广泛的的变换是离散余弦变换(DCT)同时也是是K-L的最佳替代者。此外,和傅里叶变换相比,DCT变换还有其快速算法,大大提升了计算速度。因而广泛应用了DCT变换,并且许多图像编码国际标准都以DCT变换为核心。
协方差矩阵的特征值和特征向量这两个物理量,庞大的计算量使这种变化难以得到应用。综上所述,最优且应用最广泛的的变换是离散余弦变换(DCT)同时也是是K-L的最佳替代者。此外,和傅里叶变换相比,DCT变换还有其快速算法,大大提升了计算速度。因而广泛应用了DCT变换,并且许多图像编码国际标准都以DCT变换为核心。
1.4 定向DCT的研究意义及其国内外现状
方向性信息是多维信号的一个独有的特点。目前,在图像处理应用领域,方向信息的重要性已经得到了认可,基于图像方向性的研究逐渐增多。变换的作用是使变换后的数据分布范围发生变化,使原来分布范围相对大的变得相对小,从而使变换后数据的熵较变换前相对减少,编码的平均码长相对缩短,有利于数据压缩。
利用图像的方向性信息来对其进行压缩编码,已经见于一些学者的研究,成为这一领域的一个研究热点。在基于上下文的图像编码中,为了开发一种基于广义正交变换的任意形状对象的有效图像编码方法将方向性信息被扩展为区域信息。随后,一种被称为“形状自适应离散余弦变换”的图像编码方法诞生了,从而能够对各种各样的图像片段进行编码处理。
与此同时,方向性滤波器组与小波变换提供了更好的编码质量,但是是由低分辨率子带来的,图像质量会下降。进入本世纪初,一些学者提出的斜坐标[2]DCT变换也得到了重视,它能有效的利用图像块的边缘信息。斜坐标DCT除了定义大小为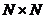 的方块图像块外,还定义了三种新的形状块:矩形、三角形和菱形,其中相邻的两个三角形状块将合并成一个菱形块。与其相比,本文研究了一种真正的方向性DCT变换,这种方法可以根据图像块中最主导的方向边缘信息来选择沿最匹配的方向进行DCT变换编码。并且该变换能够完全被限制在每个
的方块图像块外,还定义了三种新的形状块:矩形、三角形和菱形,其中相邻的两个三角形状块将合并成一个菱形块。与其相比,本文研究了一种真正的方向性DCT变换,这种方法可以根据图像块中最主导的方向边缘信息来选择沿最匹配的方向进行DCT变换编码。并且该变换能够完全被限制在每个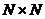 图像块区域内,可以与当前的图像压缩标准相兼容。
图像块区域内,可以与当前的图像压缩标准相兼容。
目前看来,被广泛应用于数字信号处理的各个领域以DCT为代表的正交变换的理论已经发展的相当成熟。当前所有的数字图像压缩标准中,大多采用DCT变换。但DCT也有一些难以克服的问题,由于DCT变换前会对图像进行分割造成了块边缘的不连续性,这种现象也叫做块效应[3],它严重影响了视觉效果。
因此,本文在研究DCT变换基础上,提出了定向DCT变换。
第2章 离散余弦变换原理及实现
2.1 JPEG的图像压缩基本系统
JPEG基本系统采用基于DCT的顺序编码的基本工作模式。实际上,许多硬件JPEG编码器和商用JPEG软件,支持这种工作模式。在JPEG图形压缩算法中,其基本原理是:首先将输入图片分割成 或者
或者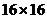 的小块,然后计算每一小块的二维离散余弦变换,进行量化、编码。传输后,JPEG接收端解码量化了的DCT系数,计算每一块逆二维离散余弦变换,然后重组这些小块构成一幅图像。通常,经过变换后大部分DCT系数都近似为0,因此,这些系数对重构的影响很小,进而可以忽略不计。
的小块,然后计算每一小块的二维离散余弦变换,进行量化、编码。传输后,JPEG接收端解码量化了的DCT系数,计算每一块逆二维离散余弦变换,然后重组这些小块构成一幅图像。通常,经过变换后大部分DCT系数都近似为0,因此,这些系数对重构的影响很小,进而可以忽略不计。
在JPEG图形压缩算法中经过离散余弦变换后大部分DCT系数都近似为0,因此,这些系数对重构的影响很小,进而可以忽略不计[4],提高图像恢复质量。
在基本工作模式下,JPEG的编码器与解码器的方框图如图2.1和2.2所示。
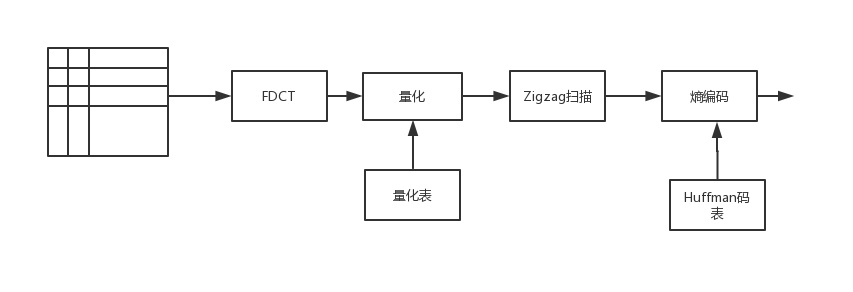
图2.1 编码器
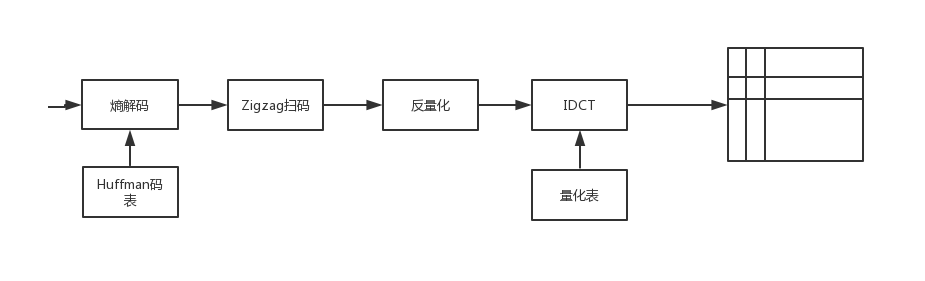
图2.2 解码器
依据图2.1和图2.2可以看出,编码时,输入源图像被分为 的像素图像块,每个块按从左到右、从上到下的顺序分别进行前向DCT变换、量化和熵编码三个基本步骤对图像进行压缩处理。所以,基于DCT的JPEG基本系统操作可分为以下三个步骤[5]:先使用DCT去除数据间的相关性;再为了实现数据压缩通过量化降低变换系数,且量化后的结果人眼基本无法识别;最后为了进一步消除数据间的统计相关性,编码直流系数和交流系数。为了减少图像间的冗余,熵编码推荐使用Huffman可变字长编码[6],然后形成压缩图像。解码时,将编码的过程反过来即可,最后得到重建图像。
的像素图像块,每个块按从左到右、从上到下的顺序分别进行前向DCT变换、量化和熵编码三个基本步骤对图像进行压缩处理。所以,基于DCT的JPEG基本系统操作可分为以下三个步骤[5]:先使用DCT去除数据间的相关性;再为了实现数据压缩通过量化降低变换系数,且量化后的结果人眼基本无法识别;最后为了进一步消除数据间的统计相关性,编码直流系数和交流系数。为了减少图像间的冗余,熵编码推荐使用Huffman可变字长编码[6],然后形成压缩图像。解码时,将编码的过程反过来即可,最后得到重建图像。
2.2 离散余弦变换[7]
当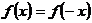 时,说明此函数为实偶函数,此时它的傅里叶变换为:
时,说明此函数为实偶函数,此时它的傅里叶变换为:
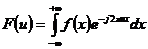
以上是毕业论文大纲或资料介绍,该课题完整毕业论文、开题报告、任务书、程序设计、图纸设计等资料请添加微信获取,微信号:bysjorg。
相关图片展示: