基于离散偶极子模型模拟小粒子的散射场开题报告
2020-02-10 23:37:28
1. 研究目的与意义(文献综述)
离散偶极近似(discrete dipoleapproximation dda)是一种用来计算任意尺寸和形状的粒子的散射场及电磁场的方法[1]。这种方法将小粒子看作是由多个可极化的立方体所组成,若立方体的尺寸远小于波长,则可将其视为偶极子,从而使用足够多的偶极子阵列来模拟物体[2]。在入射电磁波的诱导下,这些偶极子发生极化,我们通过求解偶极子的极化度便可得到物体的电磁散射特性。
电动力学中,计算物体对电磁波的散射、吸收程度,其实是在求解物体内部及周围的空间的电磁场的分布[2]。麦克斯韦方程组在理论上可以求解有介质的情况下的电场线分布,然而,因为其复杂性,只能在对称的体系中才能得到解析解[3]。所以,对于一般的物体,通常采用数值近似的方法求其周围的电磁场分布情况。离散偶极近似正是这样的方法[4]。
1964年,howard devoe建立了dda的体系结构,并发展成了一种经典的物理模型[5]。可是,在他的论文中,描述偶极子间电场作用时用的静电场表达式,而不是振荡偶极子的电场。
2. 研究的基本内容与方案
研究目标:基于离散偶极子模型以及偶极子的辐射场公式来计算小粒子的散射场。
基本内容:1.了解离散偶极子模型的概念、发展概况;2. 深入学习离散偶极子法,推导粒子散射场的计算公式;3.基于matlab编程,计算球形小粒子的散射场,讨论离散偶极子法中偶极子数量对结果收敛性的影响,以及不同迭代算法(共轭梯度法和双共轭梯度法)的计算效率。
技术方案:将小粒子分解成间距为d的立方体格点上的偶极子,偶极子的半径为r。因为偶极子的体积之和等于粒子的体积,所以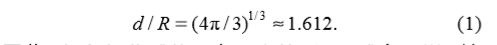
3. 研究计划与安排
第1-3周:查阅相关文献资料,明确研究内容,了解研究所需matlab编程及离散偶极子的知识。确定方案,完成开题报告。
第4-5周:对收集到的材料进行整合,撰写中英文摘要,提炼出论文的大纲。
第6-8周:编写程序,进行仿真,查找资料解决中途出现的问题。
4. 参考文献(12篇以上)
[1] 徐强,潘丰,白进强,等.离散偶极子法研究雾霾随机团簇粒子的光散射特性[j].大气与环境光学学报,2018,13(5):370-377.
[2] 朱玲,俞大鹏.采用离散偶极子近似(dda)方法研究渐变锥形金属纳米结构的超聚焦效应[j].科学通报,2009,54(12):1687-1692.
[3] m.a. yurkin,a.g.hoekstra.the discrete dipole approximation: anoverview and recent developments [j].journalof quantitative spectroscopy,2007,403(1089):558-589.




